Engineering Determine the capacitance between two surfaces

[goohu]

Homework Statement

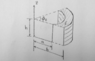
Determine capacitance between the two surfaces (see picture). The electric field is assumed to be radial.

Relevant Equations

1) C = Q/V. 2) Gauss law (cylinder); Qenc = integral of E*e0 dA , where dA is small element of the surface. 3) V = -gradient of E

For my solution I'm skipping writing out all the vectors, I just want to see if I'm in the right way or totally off.

Attempt at solution:
Qenc = ∫ E(r)*e0 ds = ∫ E(r)*e0 *h* r*dtheta, we integrate from 0 to phi0. This will give us Q = E(r)*e0*h*r*phi0.

Now we find V by integrating E from a to b with respect to r.
V = ∫ E(r) dr = Q / (e0*h*phi0) * ∫ 1/r dr = Q * ln(b/a) * 1/(e0*h*phi0).

And lastly we have C = Q/V = ln(b/a) * 1(e0*h*phi0).

Does this look reasonable? Unfortunately I don't have the right answer to this task.

 

[mitochan]

Just a small correction on

And lastly we have C = Q/V = ln(b/a) * 1(e0*h*phi0).

C=\epsilon_0 \frac{h \phi_0}{ln\frac{b}{a}}

 

[Anti Hydrogen]

I could be wrong but, why are you using gauss law for this charge distribution, I don't see any symmetry in this problem for a gaussian surface to be applied

 

[mitochan]

If the surfaces are not $\phi_0$ parts but 2$\pi$ full cylinders, are you all right on symmetry ?

 

[goohu]

Yeah, actually in this case it doesn't seem to be symmetrical so my attempt was probably wrong.

If the cylinders are whole (2 pi angle) then it is symmetrical.

 

[mitochan]

If the cylinders are whole (2 pi angle) then it is symmetrical.

By symmetry you get conductance of whole cylinders that is #2 answer with $\phi_0=2\pi$
Then cut the cake or pizza of thus charged cylinders with $\phi_0$ and $2\pi-\phi_0$ parts.
Conductance is divided to the parts with the ratio of $\phi_0$ and $2\pi-\phi_0$.