Determine the transfer function of the block diagram

In summary, the conversation discusses the reduction of a block diagram, with the resulting term being named "F". The next step involves two terms being fed into a summing point, with the resulting term being named "K". The diagram can be further reduced using the same method as in the first step. However, there is a disagreement on whether to add or subtract G3, with one person agreeing with subtracting it.
  • #1
icesalmon
270
13
Homework Statement
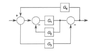
Determine the transfer function of the block diagram
Relevant Equations
Equations for Block Diagram Algebra
Step 1: I first started by reducing the inside of the block diagram of picture "bd" (the portion with G1 and the negative feedback G2)
I obtained G1/[1 + G1G2]
I'll call this term "F"

Step 2: Then I'm left with two terms feeding into a summing point:
F - G3
I'll call this term "K"

I can reduce this diagram as I did in the first step:

T(s) = K / [1 - K*G4 ]

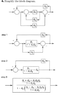
The solution, on the other hand, is adding G3 to F as indicated in the second picture I've attached
"bd2"
I am not sure if this is a mistake (to add G3 instead of subtracting it) or if I'm not seeing something.
Any help is appreciated, apologies if I've left anything out or made my solution unclear in anyway.
 

Attachments

  • bd.PNG
    bd.PNG
    8.7 KB · Views: 178
  • bd2.PNG
    bd2.PNG
    34.3 KB · Views: 160
  • Like
Likes Joshy
Physics news on Phys.org
  • #2
Has your class covered Mason's gain formula?
 
  • Like
Likes ammarb32
  • #3
No, we haven't covered that yet
 
  • #4
Giving it another look... I personally agree with you with subtracting ##G_3##.
 
  • Like
Likes icesalmon
  • #5
Joshy said:
Giving it another look... I personally agree with you with subtracting ##G_3##.
any luck? I think the solution is making a mistake.
 

FAQ: Determine the transfer function of the block diagram

What is a transfer function?

A transfer function is a mathematical representation of the relationship between the input and output of a system. It describes how the output of a system changes in response to changes in the input.

How is a transfer function determined from a block diagram?

To determine the transfer function from a block diagram, you need to apply the rules of block diagram algebra. This involves simplifying the diagram by combining blocks and then using the resulting diagram to write an equation for the output in terms of the input. This equation is the transfer function.

What is the purpose of determining the transfer function of a block diagram?

Determining the transfer function of a block diagram allows us to understand and analyze the behavior of a system. It helps us to predict how the system will respond to different inputs and to design controllers or other components to achieve a desired output.

Can the transfer function change over time?

Yes, the transfer function can change over time if the system is dynamic, meaning it changes or evolves over time. In this case, the transfer function will also change to reflect the changing behavior of the system.

Are there any limitations to determining the transfer function of a block diagram?

Yes, there are some limitations to determining the transfer function of a block diagram. It assumes that the system is linear, time-invariant, and causal. It also assumes that the system is described by a finite number of differential equations. If any of these assumptions are not met, the transfer function may not accurately represent the behavior of the system.

Similar threads

Oven controller block diagram, transfer function and temperature calcs
Replies
24
Views
4K
Engineering Transfer function to block diagram
Replies
1
Views
1K
Control systems block diagram reduction
Replies
1
Views
2K
Control System: Find the Transfer Function From Block Diagram
Replies
5
Views
2K
Engineering How do I draw the Bode diagram of this transfer function?
Replies
3
Views
2K
Transfer Function of Block Diagram
Replies
1
Views
2K
What is the Well-Known Feedback Expression for Block Diagram Manipulation?
Replies
3
Views
3K
Block diagrams to transfer functions
Replies
4
Views
2K
Block Diagram of Transfer function
Replies
5
Views
7K
Block Diagram Reduction - Control Systems Engineering
Replies
2
Views
6K

Hot Threads

Recent Insights

Back
Top