Determining total impedance, Voltage V2 and current IL of circuit

[johnsy1312]

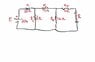
I am asked to find the total impendance ZT, voltage V2 and IL for the circuit attached

I am not sure if i am correct, but this is how i approached this problem:

So i first found the total impendance in the first parallel branch and then the second
Z=\frac{1}{\frac{1}{4<-90^o}+\frac{1}{6<90^o}}=2.4<0^o

Then i found impendance for 2nd parallel branch:
Z=\frac{1}{\frac{1}{6.8&lt;0^o}+\frac{1}{6.8&lt;0^o}+\frac{1}{8&lt;90^o}}=8.69<66.97^o

So, ZT= 8.69&lt;66.97^o+2&lt;0^o+2.4&lt;0^o = 13.09&lt;66.97^o

Finding V2: Knowing I=4mA&lt;0^o, Z_T=13.09&lt;66.97^o

E=4&lt;0^o*13.09&lt;66.97^o=52.36V&lt;66.97^o

Therefore V_2=52.36V&lt;66.97^o

Finding I_L
I_L = \frac{V_L}{Z_L}=\frac{52.36&lt;66.97^o}{8&lt;90^o}=5.76&lt;23.03^o mA

 

[gneill]

Redo your calculations for the parallel branch impedances. The formulas look good but your results do not look right. For example, for the first parallel group you have two purely reactive components (inductor and capacitor) in parallel. The resulting combined impedance should be purely imaginary, yet you've come up with purely real result (angle 0°). So something's going awry with your calculations.

 

[johnsy1312]

Redo your calculations for the parallel branch impedances. The formulas look good but your results do not look right. For example, for the first parallel group you have two purely reactive components (inductor and capacitor) in parallel. The resulting combined impedance should be purely imaginary, yet you've come up with purely real result (angle 0°). So something's going awry with your calculations.

When you add the two reactive components together, the angle becomes 90, since the inductor is 6kohm<90 and capacitor is 4kohm<-90?

 

[gneill]

When you add the two reactive components together, the angle becomes 90, since the inductor is 6kohm<90 and capacitor is 4kohm<-90?

Are you asking, concluding, or guessing? Why not show your calculation steps?

For the first parallel combination both components are reactive (so their impedances have only imaginary components). Carrying out the arithmetic should be fairly straightforward.

 

[johnsy1312]

Are you asking, concluding, or guessing? Why not show your calculation steps?

For the first parallel combination both components are reactive (so their impedances have only imaginary components). Carrying out the arithmetic should be fairly straightforward.

So with what your saying would the total impedance for the first branch be Z=(6-4)j, how do we obtain an angle from that when they are both on the same axis? Isn't the angle between them 0?

 

[gneill]

So with what your saying would the total impedance for the first branch be Z=(6-4)j, how do we obtain an angle from that when they are both on the same axis? Isn't the angle between them 0?

You had the right formula for parallel impedance in your first post. Just plug in the rectangular form of the impedances for the two components and carry through the math to arrive at a single value.

Note that the angle is specified with respect to the positive real axis. If the result lies along the imaginary axis then the angle must be either +90° or -90°.

 

[johnsy1312]

You had the right formula for parallel impedance in your first post.

So Z=\frac{1}{\frac{1}{6kohm&lt;90^o}+\frac{1}{4kohm&lt;-90^o}}?

 

[gneill]

So Z=\frac{1}{\frac{1}{6kohm&lt;90^o}+\frac{1}{4kohm&lt;-90^o}}?

Sure. Do the math. You might find that using rectangular form for the complex values will be convenient.

 

[johnsy1312]

z=\frac{12}{(2+3)j}<br /> =12*(\frac{1}{(2+3)j})

 

[gneill]

z=\frac{12}{(2+3)j}<br /> =12*(\frac{1}{(2+3)j})

Can you explain what the above is all about? The numbers don't seem to correspond to any given in the problem statement. What are you calculating?

 

[johnsy1312]

Disregard previous post:

Correct me if i am wrong.

6kohm&lt;90^o=(6sin(90^o)+6cos(90^o))j<br /> =6j
4kohm&lt;-90^o=(4sin(-90^o)+4cos(-90^o))j<br /> =-4j

Therefore:

Z= \frac{1}{\frac{1}{6j}-\frac{1}{4j}}<br /> =-12j

 

[gneill]

Disregard previous post:

Correct me if i am wrong.

6kohm&lt;90^o=(6sin(90^o)+6cos(90^o))j<br /> =6j
4kohm&lt;-90^o=(4sin(-90^o)+4cos(-90^o))j<br /> =-4j

Therefore:

Z= \frac{1}{\frac{1}{6j}-\frac{1}{4j}}<br /> =-12j

That's better! Note that the units of the result are kΩ.

Can you do the same for the second parallel grouping?

 

[johnsy1312]

Thanks!

I also have this other problem which i cannot see to get right and i have attempted it 100 times :/

I have to determine the Thevenin's equivalent circuit for the circuit attached.
I am stuck on the first and essential part, finding the thevenin's resistance.

Answer should be 10ohms, my attempt:

R_2||4 = \frac{5*16}{5+16} = 3.81ohms

R_1,3,5 = 20 + 12 + 2 = 34ohms

R_th= \frac{34*3.81}{3.81+34} = 3.42ohms

 

[gneill]

You should start a new thread for a new problem. Please do so.

One hint: R2 and R4 are not in parallel.

 

[johnsy1312]

I did :)
They look like they are in parallel though :/

 

[johnsy1312]

For this circuit, does V2=E?

 

[gneill]

For this circuit, does V2=E?

In general I won't confirm or refute unsubstantiated guesses. What logic lead you to your conclusion?

 

[johnsy123]

The parallel the branch that V2 is on seems like it is parallel to the origin source, otherwise called the current source in this case.

 

[gneill]

The parallel the branch that V2 is on seems like it is parallel to the origin source, otherwise called the current source in this case.

Sketch the "reduced" circuit, replacing the simplified parallel combinations with boxes and label them with their reduced impedances. How does the circuit look? Where does V2 appear?