Calculate the effective values in this 3-Phase Circuit

[diredragon]

Homework Statement

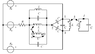
Given the known quantities $R, C, L$, $k$, and the effective values of the voltages $E_1=E_2=E_3=E$ , $w = \frac{1}{\sqrt{LC}}$ of the direct-symmetrical 3-Phase system find the expressions for the effective values of $U_{12}$, $U$ and $I$ and calculate the active power $P$ of the 3-Phase generator.

Homework Equations

3. The Attempt at a Solution [/B]
Let me write down the solutions to this problem so we know what to aim for when solving it:

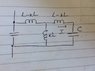
I feel kinda overwhelmed to not even know where to start from. I think can express the current $I_2$ of the generator $E_2$ in terms of the total impedance of the middle part and the voltage $U$.

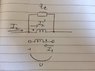
$U=jwI_1L+jwkLI'_2 => I'_2 = \frac{U}{jwkL}$ since $I_1=0$. The $Z_e$ in the diagram equals $Z_e = jwL||\frac{1}{2jwC} = -jwL$.
The current $I'_2 = I_2\frac{Z_e}{Z_e+L} => I_2 = \frac{U(k-jw)}{kLw^2}$ and this is all i can get out of this first part. I could also make the left part like this:

But i don't see how that would help. What am i missing? Is there a course of action to take that i don’t see here?

 

[cnh1995]

First look at the middle LC network. One of the coupled inductors is open-circuited, so it won't have any effect on the main circuit. That leaves you with 2 Ls and 2 Cs, all in parallel. What would be their effective reactance?

 

[diredragon]

First look at the middle LC network. One of the coupled inductors is open-circuited, so it won't have any effect on the main circuit. That leaves you with 2 Ls and 2 Cs, all in parallel. What would be their effective reactance?

I get $\frac{jwL}{2}||\frac{1}{2jwC} = \frac{-jwL}{2(1-wL)} = \frac{-jL}{2(\sqrt{LC}-L)}$

 

[cnh1995]

No.

What can you say about X_c and X_L given that ω=1/√LC? What would be the equivalent reactance of the LC network?

 

[diredragon]

No.

What can you say about X_c and X_L given that ω=1/√LC? What would be the equivalent reactance of the LC network?

Oh, $X_L = X_C$. So at the points where $Z_e$ should be is open circuit, no current $I_2$ in that branch and since the only resistive element is in that branch that explains $P = P_R = 0$. The voltage on the two capacitors must be the same as the same current goes through them and that's how i got $U_{12}$. One thing about $I$, is there an easier way than to turn this into a 3 inductors on the right side as drawn on the picture in the original post?