Electrical Engineering - Circuits - FET Transistor - Voltage Divider

[GreenPrint]

Homework Statement

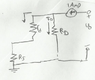
Find the voltage gain A_{v}

http://imageshack.com/a/img692/3117/qkwp.png

Homework Equations

The Attempt at a Solution

Is this the correct small signal equivalent?

http://imageshack.com/a/img203/5812/1yfe.png

I'm trying to find the output impedance Z_{O} but can't seem to derive the correct output voltage?

Apparently
i_{O} = i_{D}(1 + g_{m}R_{S} + \frac{R_{D} + R_{S}}{r_{d}})

I'm trying to solve for the output voltage using
A_{v} = \frac{v_{O}}{i_{O}} = \frac{i_{D}R_{D}}{i_{O}}

I'm trying to find a expression in which i_{O} is a function of i_{D} and the resistors etc and try to get i_{D} to cancel out so that way I can calculate the output impedance.

I have a feeling that my small signal circuit is incorrect.

Thanks for any help.

 

[rude man]

Your equiv. ckt. looks OK.

To find Zout, open all independent current sources, inject a voltage v at the output and record the current i. Then Zout = v/i.

So do that with your equiv. ckt.

To get the gain you need to compute g_m which is di/dv_gs for which you need the device's I vs. Vgs or I vs. Vds characteristic curves.

 

[rude man]

Nifty FET link:

http://acpce.org/httpdocs/StudyMaterial-SE/FET-Basics-1.ppt#357,2,Types of Field Effect Transistors (The Classification)

 

[GreenPrint]

Well when I open the current source Z = r_{d}||R_{D} and the current is Z_{O} = \frac{v_{O}}{r_{d}||R_{D}}

hm ok.

 

[rude man]

Well when I open the current source Z = r_{d}||R_{D} and the current is Z_{O} = \frac{v_{O}}{r_{d}||R_{D}}

hm ok.

Yes indeed.

 

[gneill]

Pardon my intrusion, but it looks as though the source resistor isn't AC bypassed by a capacitor, so shouldn't your r_d connect directly to the source terminal rather than ground?

 

[rude man]

gneill is right.
So you (Greenprint) need to look again at Zo. Use the same technique I suggested in post 2. The change is not big but we do want to be correct.

@g: Thanks.

 

[GreenPrint]

Well in this case shouldn't this configuration be exactly the same as a self-bias JFET configuration with R_{S} unbypassed, instead of R_{G} we have R_{Th}? I know that for a self-bias JFET configuration with R_{S} unbypassed

Z_{O} = \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r+{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D}

I believe the answer for the problem though is

\frac{R_{D}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}

Why is there a difference?

 

[The Electrician]

Well in this case shouldn't this configuration be exactly the same as a self-bias JFET configuration with R_{S} unbypassed, instead of R_{G} we have R_{Th}? I know that for a self-bias JFET configuration with R_{S} unbypassed

Z_{O} = \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r+{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D}

I believe the answer for the problem though is

\frac{R_{D}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}

Why is there a difference?

Why do you think the answer is \frac{R_{D}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}?

What would the answer be if rd were missing? If it were ∞ in other words?

Now look at both expressions and ask yourself what would the limit of each expression be as rd→∞?

 

[GreenPrint]

Well if r_{d} is connect to the source then the small signal equivalent circuit for a voltage diver unbypassed R_{S} is exactly the same as the small signal equivalent circuit for a self-bias configuration unbypassed R_{S} if we treat R_{Th} as R_{G}

The formula for the output impedance Z_{O} for a self-bias configuration unbypassed R_{S} is

Z_{O} = \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r_{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D}

if we take the limit

Z_{O} \stackrel{lim}{r_{d} → ∞} = \stackrel{lim}{r_{d} → ∞} \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r_{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D} = R_{D}

Am I really suppose to go with this as the output impedance Z_{O}?

The solutions manual from a previous version has this for the answer.

http://imageshack.com/a/img14/6652/3jn9.png

I know it could be a different problem but it looks like the same exact problem with a different value for r_{d}

 

[rude man]

Well in this case shouldn't this configuration be exactly the same as a self-bias JFET configuration with R_{S} unbypassed, instead of R_{G} we have R_{Th}? I know that for a self-bias JFET configuration with R_{S} unbypassed

Z_{O} = \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r+{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D}

I believe the answer for the problem though is

\frac{R_{D}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}

Why is there a difference?

If your expression for Zout for an unbypassed common-source config. is right then obviously someone decided that R_S(g_m + 1/r_d) << 1. Why don't you plug in the numbers and verify that that approximation is valid.

And in fact if that approx. is valid then you can reduce the expression for Zout further, to a very simple function of just R_D and r_d.

EDIT: looking at your numbers, g_mR_s = 3.3 which is not << 1 so obviously your supposed answer can't be right. So stick with the unbypassed C/S expression.

 

[GreenPrint]

Well isn't

g_{m} = \frac{2I_{DSS}}{V_{P}}(1 - \frac{V_{GS}}{V_{P}})?

the only problem is that I don't know V_{GS} and it's not given, and I'm not sure how to find this value. You see above it says "as before" but I have looked and they don't ever show how they got the value.

 

[The Electrician]

Well if r_{d} is connect to the source then the small signal equivalent circuit for a voltage diver unbypassed R_{S} is exactly the same as the small signal equivalent circuit for a self-bias configuration unbypassed R_{S} if we treat R_{Th} as R_{G}

The formula for the output impedance Z_{O} for a self-bias configuration unbypassed R_{S} is

Z_{O} = \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r_{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D}

if we take the limit

Z_{O} \stackrel{lim}{r_{d} → ∞} = \stackrel{lim}{r_{d} → ∞} \frac{1 + g_{m}R_{S} + \frac{R_{S}}{r_{d}}}{1 + g_{m}R_{S} + \frac{R_{S} + R_{D}}{r_{d}}}R_{D} = R_{D}

Am I really suppose to go with this as the output impedance Z_{O}?

The solutions manual from a previous version has this for the answer.

http://imageshack.com/a/img14/6652/3jn9.png

I know it could be a different problem but it looks like the same exact problem with a different value for r_{d}

The purpose of taking limits is not to find Zo, or that Zo is RD.

You had two possible expressions for Zo. One way to tell which is correct is this:

You know what Zo would be if there were no rd; it would be just RD. So whatever expression you come up with, it must reduce to just RD if you take the limit of the expression when rd→∞.

The second expression's limit is \frac{R_{D}}{1 + g_{m}R_{S}}, which is not just RD.

The first expression's limit is just RD.

These two limits don't prove that the first expression is correct; they prove that the second expression is wrong. So, if you knew that the correct answer was one of the two expressions, taking these limits rules out the second one. This is just an aid, like checking units, to help you rule out a wrong result.

Now, if we substitute numerical values into the expressions, we get:

and:

The numerical evaluations are very different; the second is not even a very good approximation to the first.

Have you tried analyzing the circuit to determine Zo? rude man already suggested that you inject a test signal at the output node.

If you set up the KCL equation(s) and inject a 1 amp signal at the output node, the voltage there will be numerically equal to the impedance there. Do it symbolically and substitute numbers once you have a symbolic expression for Zo.

 

[rude man]

Well isn't

g_{m} = \frac{2I_{DSS}}{V_{P}}(1 - \frac{V_{GS}}{V_{P}})?

the only problem is that I don't know V_{GS} and it's not given, and I'm not sure how to find this value. You see above it says "as before" but I have looked and they don't ever show how they got the value.

They must give you something abou the JFET. Like I_DSS and V_P? Where did you dig up your g_m and r_d?
?

 

[The Electrician]

They must give you something abou the JFET. Like I_DSS and V_P? Where did you dig up your g_m and r_d?
?

Look at the first post. Idss, Vp and rd are given on the schematic. All GreenPrint has to do is look up the relevant formulas for Id vs. Vgs; then he can calculate the Q point for this circuit.

 

[rude man]

Well isn't

g_{m} = \frac{2I_{DSS}}{V_{P}}(1 - \frac{V_{GS}}{V_{P}})?

the only problem is that I don't know V_{GS} and it's not given, and I'm not sure how to find this value. You see above it says "as before" but I have looked and they don't ever show how they got the value.

You do have I_DSS and V_P. You can compute V_GS by using the standard JFET equation for i and equating i to the current thru R_S.

 

[GreenPrint]

So then Z_{O} = \frac{1}{R_{D}||(r_{d} + R_{S}}).

 

[GreenPrint]

Oh you mean find V_{GS} using I_{D} = I_{DSS}(1 - \frac{V_{GS}}{V_{P}})^{2}

equating the current I_{D} as the current through R_{S} some how?

 

[The Electrician]

So then Z_{O} = \frac{1}{R_{D}||(r_{d} + R_{S}}).

How did you get this? You know that gm has to be involved in there.

 

[GreenPrint]

I opened up the current source g_{m}V_{gs} applied a test current of 1 A at V_{O} and found V_{O} using R_{D} in parallel with r_{d} in series with R_{s}

See the attached picture

 

[rude man]

So then Z_{O} = \frac{1}{R_{D}||(r_{d} + R_{S}}).

No. Why aren't you using your formua for the unbypassed R_S?

 

[rude man]

I opened up the current source g_{m}V_{gs} applied a test current of 1 A at V_{O} and found V_{O} using R_{D} in parallel with r_{d} in series with R_{s}

See the attached picture

You can't 'open up' the current source because v_gs is not zero if you apply a test voltage to the output to obtain Z_o. r_d affects v_s so then v_gs is affected too.

 

[rude man]

Oh you mean find V_{GS} using I_{D} = I_{DSS}(1 - \frac{V_{GS}}{V_{P}})^{2}

equating the current I_{D} as the current through R_{S} some how?

Exactly! Whaddaya mean, 'somehow'? You have I_D and you have R_S, so what do you suppose V_S = ? Like, volts = current times ohms?

Remember, V_GS = V_G - V_S and you can figure out V_G from your schematic diagram.

 

[GreenPrint]

but I thought I_D didn't go through R_S? but went through R_D?

 

[rude man]

but I thought I_D didn't go through R_S? but went through R_D?

Well, where do you think I_D goes? It has to return to ground and it's not going backwards thru the gate! Look at your schematic, post 1!

For a JFET, I_D = I_S.

 

[GreenPrint]

So then V_{GS} is about -.974 V?The equation looks like a pain in the but to solve algebraically so i graphed it.

 

[GreenPrint]

No. Why aren't you using your formua for the unbypassed R_S?

That is indeed the correct formula?

 

[GreenPrint]

My answer key says Z_{O} = r_{d}||R_{D} which I think is wrong?

 

[rude man]

That is indeed the correct formula?

Well, I solved for Zout using your equiv. ckt. but it's too tedious to figure out if my and your expressions are the same.

Where did you get your expression from? Why do you doubt that it's right?

 

[rude man]

My answer key says Z_{O} = r_{d}||R_{D} which I think is wrong?

.

Yes, it's wrong.
It would be right if R_S were bypassed with a big capacitor.