Valerie Witchy
- 3
- 0
Summary:: the set of arrays of real numbers (a11, a21, a12, a22), addition and scalar multiplication defined by ; determine whether the set is a vector space; associative law
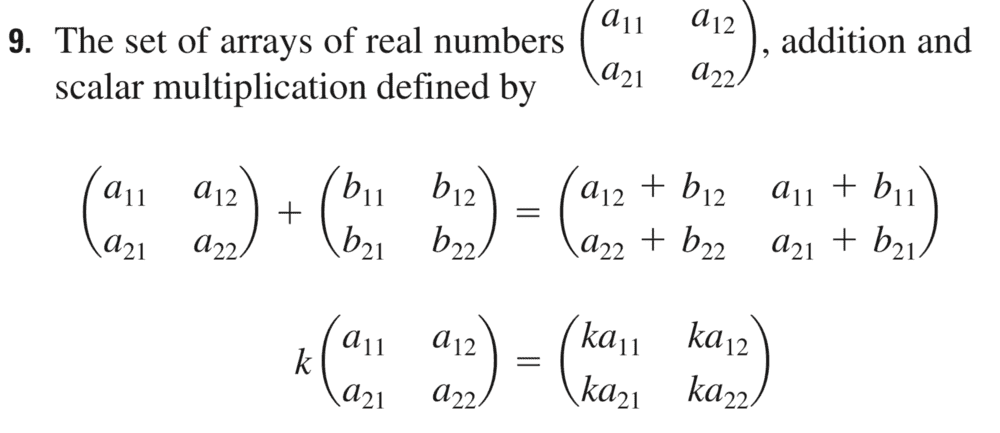
Question: determine whether the set is a vector space.
The answer in the solution books I found online says that the set is a vector space. However I do not think the set satisfies the associative law of vector addition:
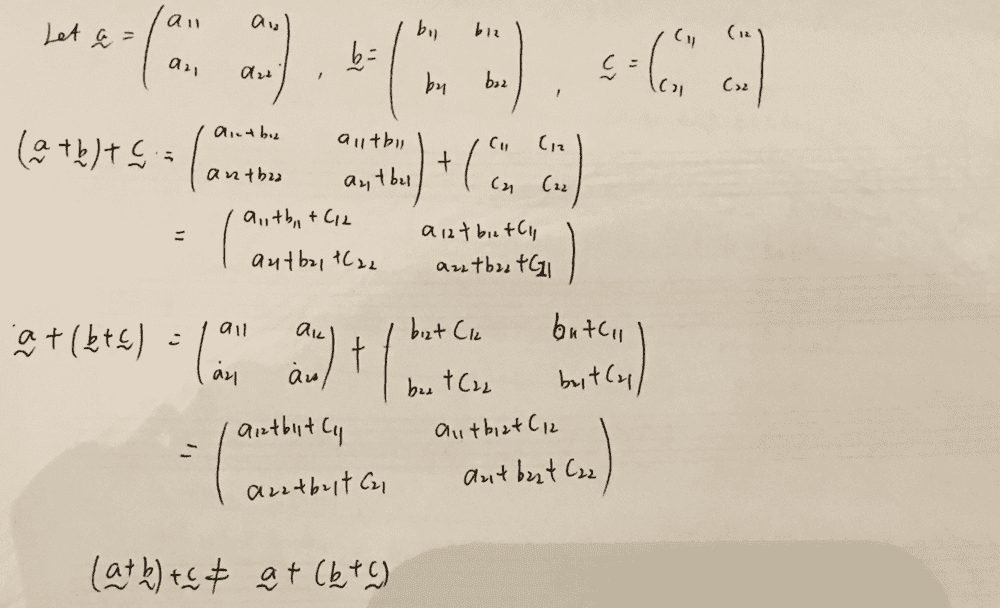
Can anyone tell me where did I go wrong?
Question: determine whether the set is a vector space.
The answer in the solution books I found online says that the set is a vector space. However I do not think the set satisfies the associative law of vector addition:
Can anyone tell me where did I go wrong?