Develop Model Emulating Given Wave Pattern

[ausmate]

Question:
Develop a model for producing a repeating pattern of 8 waves, with 6 smaller waves of approx. the same size and the second and sixth waves much larger. The sketch below gives a general indication of the eight wave pattern.

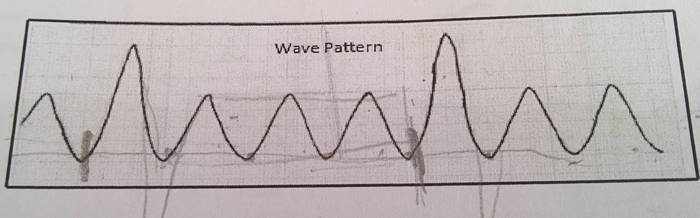
(Sorry for large image)

I would like to know how to "take a shot" at it, the solution must be a sine function. Can be generic, by that I mean no definite amplitude, only that the model clearly resemble the one given.

I have tried to emulate it by trial and error, combining functions such as in the form [y=sin x + 0.3sin3x] with no luck.

Thanks in advance,
-Ausmate

 

[Mentallic]

All I could come up with was a relatively complicated solution which is of the form

y=sin(x)+k(x)s(x)

where k(x) is equal to 1 everywhere that you want the amplitude of sin(x) to be higher, and 0 everywhere else. s(x) is a function that uses sin(x)^2 because it has a derivative of 0 where it touches the x-axis.

k(x)=\frac{1}{2}\left(\frac{|r|}{r}+1\right)

where

r=\sin{\left(\frac{x+3\pi/2}{4}\right)}-\frac{1}{\sqrt{2}}

and I'll leave s(x) to you if you're interested in pursuing this further.