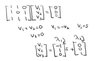hpayandah
- 18
- 0
Homework Statement
I think my teacher made a mistake in his homework answer. I need to verify this for practice. The answer I got is below. The answer the teacher has is in the pdf.
Homework Equations
Please refer to attached pdf
The Attempt at a Solution
So there is two eigenvalues= 4 and 2
but the eigenvalue 2 has 2 eigenvectors [-1 1 0]T and [0 0 1]T but my teacher has only one [-1 1 0]T. That's why he says A is not diagonalizable. Do you think it's correct?