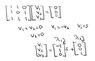Homework Help Overview
The discussion revolves around the diagonalization of a matrix based on its eigenvalues and eigenvectors. The original poster questions the correctness of their teacher's answer regarding the diagonalizability of a matrix with eigenvalues 4 and 2, specifically focusing on the eigenvectors associated with the eigenvalue 2.
Discussion Character
- Conceptual clarification, Assumption checking, Problem interpretation
Approaches and Questions Raised
- The original poster presents their findings on eigenvalues and eigenvectors, questioning the teacher's assertion about diagonalizability. Some participants verify the teacher's result and discuss the implications of having fewer eigenvectors than the dimension of the matrix. Others challenge the validity of certain eigenvectors and the steps taken to derive them.
Discussion Status
Contextual Notes
Participants are working with a 3x3 matrix and discussing the requirement for three linearly independent eigenvectors for diagonalizability. There is mention of a pdf with the teacher's answer, which is not present in the discussion.