Different Blackbody Intensity Peaks, how do we measure it?

[tade]

For the Blackbody Spectrum, there are two versions of the formula, one for wavelength and the other one for frequency:

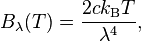
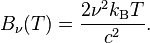
The peak intensities for both occur at different wavelengths (or frequencies).How do scientists measure the spectral radiance of blackbodies?

Are there TWO types of equipment, one for $$B_\lambda$$ and the other for $$B_\nu$$, such that each device yields a peak at a different frequency?

 

[drvrm]

How do scientists measure the spectral radiance of blackbodies?

Are there TWO types of equipment, one for

BλBλ​

B_\lambda and the other for

BνBν​

B_\nu, such that each device yields a peak at a different frequency?

as frequency and wavelengths are related by c= frequency x wavelength ,where c is the velocity of light , one may not need two types of experiments to measure intensity variation with either wavelength or frequency.
just an example of measurement technique;
For the experiment, a tungsten filament light bulb was used as the emitting source.
The filament, in conjunction with an apparatus that could record the relative intensity of light at various frequencies or wavelength, . The apparatus used contained a tungsten filament light as the black body emitter, a diffraction grating to separate the various wavelengths of light and a photodiode to detect relative intensities of incident light.
reference;https://www.phys.ksu.edu/personal/rprice/BB.pdf

 

[tade]

But then how would we obtain the two different peak values?

 

[drvrm]

But then how would we obtain the two different peak values?

does any experimental curve give different peak value for a wavelength and corresponding frequency?
pl. quote results.
or you want to say that c=nx wavelength does not hold experimentally?

 

[drvrm]

The peak intensities for both occur at different wavelengths (or frequencies).

your formula may be incorrect or depicting some other parameter-not the intensities

some facts;

The amount of radiation emitted in a given frequency range should be proportional to the number of modes in that range. The best of classical physics suggested that all modes had an equal chance of being produced, and that the number of modes went up proportional to the square of the frequency.

But the predicted continual increase in radiated energy with frequency (dubbed the "ultraviolet catastrophe") did not happen. Nature knew better.

 

[tade]

You can do the math and see for yourself.

From wikipedia of Plancks law: "Evidently, the location of the peak of the spectral distribution for Planck's law depends on the choice of spectral variable"

Also, read the section "Peaks" under "Properties"

 

[vanhees71]

But then how would we obtain the two different peak values?

By maximizing the corresponding distribution functions. Where do you see a problem with that? The peak values are just rough characterizations of the distributions without much further physical significance!

 

[nasu]

What do you think these formula represent?
They don't have peaks anyway.
Do you understand what are these?

 

[Charles Link]

Any spectral density intensity function has a slightly different shape when displayed in wavelength space than it does in frequency space. These two are related by $|I_{\lambda}(\lambda)d\lambda|=|I_{\nu}(\nu)d\nu|$. where $\nu=1/\lambda$ so that $|d\nu/d\lambda |=1/\lambda^2$. It is straightforward to convert from one to the other, and most any spectroscopist has little trouble converting their experimental results to which ever form they need to compare to. You are correct that the "peaks" for the blackbody curve, (as well as any other smooth spectral function), do occur at different wavelengths for the two graphs. The energy found between any two wavelengths is the same for both graphs, and the graphs by either method are entirely consistent with each other. You may still be asking how this is done experimentally. The blackbody is often used as a calibration source, and the spectrum is measured at 100 or more spectral points. A spectrum is run for an unknown source, and then a calibration spectral run is performed over the same set of wavelengths using a calibration blackbody source (at a fixed temperature). Let $V(\lambda)$ be the detector voltage at wavelength $\lambda$. Assuming the detector responds linearly to incident energy, (which is often the case), $V_s(\lambda)/V_{bb}(\lambda)=I_s(\lambda)/I_{bb}(\lambda)$. (other geometric factors, area, distance, etc., can also be included in this formula). Depending on whether you display the results in wavelength or frequency, the appropriate blackbody spectral function $I_{bb}(\lambda)$ (or $I_{bb}(\nu)$) is inserted into the equation. It is straightforward for anyone to take a displayed graph of $I_s(\lambda)$ or $I_s(\nu)$ and convert it to the other form. One additional item is your blackbody function is not entirely correct. This may be an early proposed version or an approximation of some kind. In wavelength form, it correctly reads $L_{\lambda}(\lambda, T)=2hc^2/((\lambda^5)(exp((hc/(\lambda k T))-1))$ and $I_{\lambda}(\lambda,T)=L_{\lambda}(\lambda,T)A_{bb}$ where $A_{bb}$ is the area. (Your blackbody formulas are using $\nu=c/\lambda$ which is ok, but the formulas are not completely correct. In addition, the usual convention in spectroscopy is that $\nu=1/\lambda$.)

 

[vanhees71]

What do you think these formula represent?
They don't have peaks anyway.
Do you understand what are these?

They are distribution functions of energy per frequency or wave length, and of course they have peaks. In the Wikipedia article you find these curves!

 

[Charles Link]

They are distribution functions of energy per frequency or wave length, and of course they have peaks. In the Wikipedia article you find these curves!

As I mentioned in post #9, the formulas the OP has are incorrect, and upon closer inspection, neither of them even has a peak. The OP still asks a very good question, but would do well to start with correct blackbody formulas.

 

[nasu]

They are distribution functions of energy per frequency or wave length, and of course they have peaks. In the Wikipedia article you find these curves!

The question was for the first poster. :)

Not as they are given in the OP. These have no peak.
They may be the high temperature approximation of the complete functions.

 

[Charles Link]

The question was for the first poster. :)

Not as they are given in the OP. These have no peak.
They may be the high temperature approximation of the complete functions.

Hopefully the OP returns to see all of our inputs. :-)

 

[tade]

By maximizing the corresponding distribution functions. Where do you see a problem with that? The peak values are just rough characterizations of the distributions without much further physical significance!

I thought the peak values can be physically measured?

 

[tade]

What do you think these formula represent?
They don't have peaks anyway.
Do you understand what are these?

As I mentioned in post #9, the formulas the OP has are incorrect, and upon closer inspection, neither of them even has a peak. The OP still asks a very good question, but would do well to start with correct blackbody formulas.

You are right. I accidentally uploaded the Rayleigh-Jeans Law instead of Planck's Law. I meant to use Planck's Law.

Now it is too late to edit it though.

 

[The Bill]

Why would we need different instruments? That's like saying you'd need different rulers to measure items that are 5cm long from the one used to measure items that are 7cm long. As long as the peak of the spectrum is within the wavelength range of the spectrometer you are using, you can measure the peak. For example, the commonly used 3B student spectrometers can measure an intensity curve from 360nm to 800nm, which includes the entire visual spectrum along with a little ultraviolet and a good chunk of short infrared. That allows one to measure the peaks in the sun, common lightbulbs, and many other sources.

 

[tade]

You may still be asking how this is done experimentally. Let $V(\lambda)$ be the detector voltage at wavelength $\lambda$. Assuming the detector responds linearly to incident energy, (which is often the case), $V_s(\lambda)/V_{bb}(\lambda)=I_s(\lambda)/I_{bb}(\lambda)$. Depending on whether you display the results in wavelength or frequency, the appropriate blackbody spectral function $I_{bb}(\lambda)$ (or $I_{bb}(\nu)$) is inserted into the equation.

Thanks Charles, but I'm still confused. What do 'bb' and 's' stand for?

Why would we need different instruments?

http://qdl.scs-inc.us/2ndParty/Images/Charles/Sun/SolarSpectrum2_wbg.png
This is the solar spectrum.

For 5525 K, and following Planck's Law

, it peaks at about 524 nm.

For 5525 K, and following

, it peaks at about 325 THz, or 923 nm.

What kind of instruments allow us to obtain 524 nm And/Or 923 nm?

 

[tade]

does any experimental curve give different peak value for a wavelength and corresponding frequency?

The peak values are just rough characterizations of the distributions without much further physical significance!

Why would we need different instruments? That's like saying you'd need different rulers to measure items that are 5cm long from the one used to measure items that are 7cm long

What kind of instruments allow us to obtain 524 nm And/Or 923 nm?

drvrm, vanhees71, The Bill, any suggestions?

 

[Charles Link]

Thanks Charles, but I'm still confused. What do 'bb' and 's' stand for?
http://qdl.scs-inc.us/2ndParty/Images/Charles/Sun/SolarSpectrum2_wbg.png
This is the solar spectrum.
What kind of instruments allow us to obtain 524 nm And/Or 923 nm?

The "s" subscript stands for the unknown source whose spectrum is being measured, and "bb" is the calibration blackbody. Its temperature can be measured with a thermocouple and kept constant. Calibration blackbodies are commercially available. A typical temperature used for them is 1000 C (1273 K), and the absolute spectral intensity output is typically within +/- 1% of the Planck blackbody function. Meanwhile silicon photodiodes (also available commercially) can be used for measurements wavelengths from 400 nm to 1000 nm. Their response is not the same at all wavelengths and similarly a (diffraction grating based) spectrometer does not have the same throughput for all wavelengths, thereby the need for a complete calibration blackbody spectral run. One other interesting thing about the blackbody function is that the function integrates precisely from 0 to infinity to give the radiation per unit area $M=\sigma T^4$. (Note $M=L*\pi$ )

 

[greswd]

The "s" subscript stands for the unknown source whose spectrum is being measured, and "bb" is the calibration blackbody. Its temperature can be measured with a thermocouple and kept constant. Calibration blackbodies are commercially available. A typical temperature used for them is 1000 C (1273 K), and the absolute spectral intensity output is typically within +/- 1% of the Planck blackbody function. Meanwhile silicon photodiodes (also available commercially) can be used for measurements wavelengths from 400 nm to 1000 nm. Their response is not the same at all wavelengths and similarly a (diffraction grating based) spectrometer does not have the same throughput for all wavelengths, thereby the need for a complete calibration blackbody spectral run.

Let's say that we are measuring the solar spectrum.

We want to obtain the 524 nm and the 923 nm peaks; what is the difference in the experimental procedures for both scenarios?

 

[Charles Link]

Let's say that we are measuring the solar spectrum.

We want to obtain the 524 nm and the 923 nm peaks; what is the difference in the experimental procedures for both scenarios?

There is no experimental difference. The results can either be displayed using a graph of $I_{\lambda}(\lambda)$ vs. $\lambda$ or $I_{\nu}(\nu)$ vs. $\nu$. Anyone can take a graph of one form and generate the other. Normally a diffraction grating based spectrometer is designed to have equal wavelength increments as it steps from one wavelength to the next. The spectral points will not be equally spaced in wave number ($\nu=1/\lambda$), but experimentally there really is no difference. The measured spectrum can be presented in either fashion.

 

[greswd]

There is no experimental difference. The results can either be displayed using a graph of $I_{\lambda}(\lambda)$ vs. $\lambda$ or $I_{\nu}(\nu)$ vs. $\nu$. Anyone can take a graph of one form and generate the other.

If we only conduct one experiment, wouldn't the peaks for both graphs occur at the same wavelength, not 524 nm or 923 nm?

 

[nasu]

There is only one peak in the intensity.
However, neither formula presented in the discussion is for intensity but rather for spectral density. Intensity in a given interval would be the density multiplied by the interval (if the interval is small enough or infinitesimal). As the frequency and the wavelength interval are not related by a linear relationship ( dλ=-(c/f²)df), the two peaks of the two functions are not related by λ=c f.

 

[Charles Link]

If we only conduct one experiment, wouldn't the peaks for both graphs occur at the same wavelength, not 524 nm or 923 nm?

The peak occurs from a result of the function $I_{\lambda}(\lambda)$ or $I_{\nu}(\nu)$. The spectrometer voltage $V(\lambda)$ is likely to also peak somewhere in the vicinity of both of these, but the problem of where the spectral intensity peak occurs is very much a mathematical one. A physicist that is comfortable working in wavelength will tell you the solar spectrum peaks around 500 nm, and this is most often the result that we are given. We normally don't hear the result that the solar spectrum peaks at 900 nm. (I also need to check the arithmetic here-I didn't realize the Wien's law result for the peaks of wavelength vs. wavenumber were that far apart.)

 

[greswd]

There is only one peak in the intensity.
However, neither formula presented in the discussion is for intensity but rather for spectral density. Intensity in a given interval would be the density multiplied by the interval (if the interval is small enough or infinitesimal). As the frequency and the wavelength interval are not related by a linear relationship ( dλ=-(c/f²)df), the two peaks of the two functions are not related by λ=c f.

Thanks, now I see.

In that case, what is the mathematical function for the intensity?

 

[The Bill]

If we only conduct one experiment, wouldn't the peaks for both graphs occur at the same wavelength, not 524 nm or 923 nm?

Modern spectrometers effectively perform hundreds or thousands of what I think you are referring to as "experiments" in one measurement. Take the wavelength range of the instrument and divide it by the wavelength resolution of the instrument. The instrument produces that many useful intensity measurements.

For example, the 3B Scientific spectrometer I mentioned earlier has a range from 360nm to 800nm, which is a 440nm range. Its resolution is <2.0nm. So, a single measurement with this instrument yields approximately 220 useful intensity values along that range of spectrum. If I'm understanding you correctly, this is what you would call 220 "experiments," done in a single measurement all at once.

 

[greswd]

Modern spectrometers effectively perform hundreds or thousands of what I think you are referring to as "experiments" in one measurement. Take the wavelength range of the instrument and divide it by the wavelength resolution of the instrument. The instrument produces that many useful intensity measurements.

For example, the 3B Scientific spectrometer I mentioned earlier has a range from 360nm to 800nm, which is a 440nm range. Its resolution is <2.0nm. So, a single measurement with this instrument yields approximately 220 useful intensity values along that range of spectrum. If I'm understanding you correctly, this is what you would call 220 "experiments," done in a single measurement all at once.

That's not what I meant. But nevermind about that.

What I'm curious is, how do we measure 524 nm and 923 nm peaks?

 

[The Bill]

That's not what I meant. But nevermind about that.

What I'm curious is, how do we measure 524 nm and 923 nm peaks?

You use a spectrometer whose range includes both wavelengths, or two spectrometers which each cover one of those wavelengths. You hook the spectrometer(s) up to a computer, point the spectrometer(s) at the source, and look for peaks on the intensity vs. wavelength graph that is displayed on the spectrometer software on the computer.

 

[greswd]

The peak occurs from a result of the function $I_{\lambda}(\lambda)$ or $I_{\nu}(\nu)$. The spectrometer voltage $V(\lambda)$ is likely to also peak somewhere in the vicinity of both of these

What is the math formula of $V(\lambda)$?

A physicist that is comfortable working in wavelength will tell you the solar spectrum peaks around 500 nm, and this is most often the result that we are given. We normally don't hear the result that the solar spectrum peaks at 900 nm. (I also need to check the arithmetic here-I didn't realize the Wien's law result for the peaks of wavelength vs. wavenumber were that far apart.)

Doesn't matter that they're far apart, they're supposed to be different anyway.

 

[nasu]

What I'm curious is, how do we measure 524 nm and 923 nm peaks?

There is no 923 nm peak in the solar spectrum. None of these two formulas give such a peak.