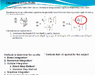
SUMMARY
The discussion centers on the derivation of the formula for gradually varied flow in open channel hydraulics, specifically the relationship between K and y. The key equation presented is Q = (1/n)(A)(R^2/3) [(s)(^0.5)], leading to K = (1/n)(b)(y^5/3). The participants clarify that K_0 corresponds to y_0, and the ratio of K to K_0 is expressed as (K_0/K)^2 = (y_0/y)^{10/3}. The confusion regarding the cancellation of variables n and b is addressed, confirming that they do not cancel out in the context of the equations discussed.
PREREQUISITES
- Understanding of open channel flow principles
- Familiarity with hydraulic equations, specifically Q = (1/n)(A)(R^2/3)
- Knowledge of the concept of hydraulic radius (R)
- Basic algebraic manipulation skills for handling equations
NEXT STEPS
- Study the derivation of the Manning's equation in detail
- Learn about the implications of gradually varied flow in hydraulic engineering
- Explore the concept of hydraulic radius and its significance in flow calculations
- Investigate the relationship between flow rate (Q) and channel geometry
USEFUL FOR
Students and professionals in civil engineering, particularly those specializing in hydraulic engineering and open channel flow analysis.