Differential pressures in a chamber, revisited and clarified

[LowEParticle]

This is a clearer, better drawn, and shorter version of a question I asked a few days ago. I apologize for not initially reducing it to this state - sometimes when reducing a question to its essence I stop too soon!

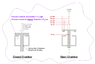
The diagram below shows two cross-sections of an axis-symmetric cylindrical chamber that has a valve armature passing through its center. The valve armature descends to close the chamber (left-hand drawing) and rises up to open the chamber (right-hand drawing). Where the valve armature's shaft passes through the bottom of the chamber it is sealed off by a frictionless, air-tight seal. The air pressure outside the chamber is always P_high. If the chamber is closed, then the air pressure inside of it is P_low.

My problem is the total force F_total on the valve armature due to differential pressure when the chamber is closed. F_total is the sum of three terms:

F₁ is the pressure inside of the chamber pressing upwards on the bottom of the valve armature plate (14mm radius):
F₁ = P_low * \pi * (14)² (upwards)

F₂ is the pressure outside of the chamber pressing upwards on the very bottom of the valve armature shaft (4mm radius):
F₂ = P_high * \pi * (4)² (upwards)

F₃ is the pressure outside of the chamber pressing downwards on the top of the valve armature plate (18mm radius):
F₃ = P_high * \pi * (18)² (downwards)

So F_total = -F₁ - F₂ + F₃

I showed all the significant radii on the right-hand drawing for easy identification, however, the solution above does not use the 20mm, 12mm, or 8mm radii. I have two questions:

1. Have I picked the correct radii to correctly calculate the relevant forces?
2. Are the 3 forces I've identified the only ones produced by differential pressures that are relevant to the caclulation of F_total?

Thank you very much for reading this and considering my problem.
Dave

 

[256bits]

well hello there,
You should re-think F1.
Does the low pressure act on the whole of the 14mm radius, or just part of it?
If you examine F2, that may give you a clue.

 

[LowEParticle]

well hello there,
You should re-think F1.
Does the low pressure act on the whole of the 14mm radius, or just part of it?
If you examine F2, that may give you a clue.

Thank you very much for finding this error! I've written the corrected description of F1 below:

F₁ is the pressure inside of the chamber pressing upwards on the bottom of the valve armature plate (14mm radius) excepting the 4mm radius of the armature shaft:
F₁ = P_low * \pi * (14² - 4²) (upwards)

I appreciate your help very much!
Dave