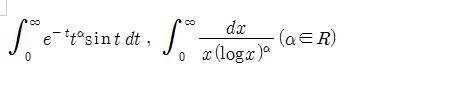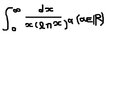- #1
bw0young0math
- 27
- 0
Hello. I'm studying improper integrals in real analysis. However, two problems are very difficult to me. If you are OK, please help me.(heart)
1.2.
View attachment 1549
I have solutions about above problems.
However, I don't know how I approach and find the way for solving them.
1.2.
View attachment 1549
I have solutions about above problems.
However, I don't know how I approach and find the way for solving them.