OhNoYaDidn't
- 25
- 0
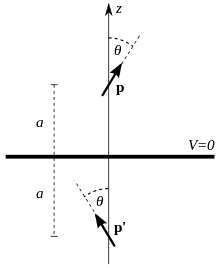
An electric dipole p with arbitrary direction and is at distance a from plane infinite conductor at z=0.
Using the image of the dipole
##p=(2pcos\theta \hat{z}+psin\theta \hat{x}##
##p'=(2p'cos\theta \hat{z}-p'sin\theta \hat{x}##
Using the following:##V=\frac{\vec{p'}.\hat{r}}{4\pi\epsilon_0{r}^2}##, i get ## V=\frac{p'(2cos\theta-sin\theta)}{4\pi\epsilon_0{r}^2}## Which i can now write as ##\vec{E}## by symple taking the gradient in spherical coordinates. I get: ##\vec{E}=p'\frac{(2cos\theta-sin\theta)\hat{r}+(2sin\theta+cos\theta)\hat{\theta}}{4\pi\epsilon_0{r}^3}##
Now using one of Maxwell's laws i can get the charge distribution: ##\rho=\epsilon_0\nabla.\vec{E}=\frac{psin\theta}{4\pi{r}^4}## Does it make any sense that this is the result for charge distribution?
Thank you guys, I'm not really sure how to interpret this
Using the image of the dipole
##p=(2pcos\theta \hat{z}+psin\theta \hat{x}##
##p'=(2p'cos\theta \hat{z}-p'sin\theta \hat{x}##
Using the following:##V=\frac{\vec{p'}.\hat{r}}{4\pi\epsilon_0{r}^2}##, i get ## V=\frac{p'(2cos\theta-sin\theta)}{4\pi\epsilon_0{r}^2}## Which i can now write as ##\vec{E}## by symple taking the gradient in spherical coordinates. I get: ##\vec{E}=p'\frac{(2cos\theta-sin\theta)\hat{r}+(2sin\theta+cos\theta)\hat{\theta}}{4\pi\epsilon_0{r}^3}##
Now using one of Maxwell's laws i can get the charge distribution: ##\rho=\epsilon_0\nabla.\vec{E}=\frac{psin\theta}{4\pi{r}^4}## Does it make any sense that this is the result for charge distribution?
Thank you guys, I'm not really sure how to interpret this