Why do we ignore the contribution to a surface integral from the point r=0?

[Mike400]

Let $V'$ be the volume of dipole distribution and $S'$ be the boundary.

The potential of a dipole distribution at a point $P$ is:

$\displaystyle\psi=-k \int_{V'} \dfrac{\vec{\nabla'}.\vec{M'}}{r}dV' +k \oint_{S'}\dfrac{\vec{M'}.\hat{n}}{r}dS'$

If $P\in V'$ and $P\in S'$, the integrand is discontinuous (infinite) at the point $r=0$. If we use spherical and polar coordinates, the integrand is continuous everywhere:

\begin{align}
\psi &=\bbox[orange,5px]{-k \int_{V'} \dfrac{\vec{\nabla'}.\vec{M'}}{r} r^2 \sin \theta\ d\theta\ d\phi\ dr}\\
&\bbox[pink,5px]{+k\oint_{S'_1} \dfrac{\vec{M'}.\hat{n}}{r} \sqrt{{f_x}^2+{f_y}^2+1}\ R\ dR\ d\theta'}
\bbox[yellow,5px]{+ k \oint_{S'_2}\dfrac{\vec{M'}.\hat{n}}{r}dS'}\\
&=\bbox[orange,5px]{-k \int_{V'} \vec{\nabla'}.\vec{M'}\ r \sin \theta\ d\theta\ d\phi\ dr}\\
&\bbox[pink,5px] {+ k \oint_{S'_1} \vec{M'}.\hat{n}\ \sqrt{{f_x}^2+{f_y}^2+1}\ \dfrac{R}{\sqrt{R^2+f^2}} dR\ d\theta'}
\bbox[yellow,5px] {+ k \oint_{S'_2}\dfrac{\vec{M'}.\hat{n}}{r}dS'}
\end{align}

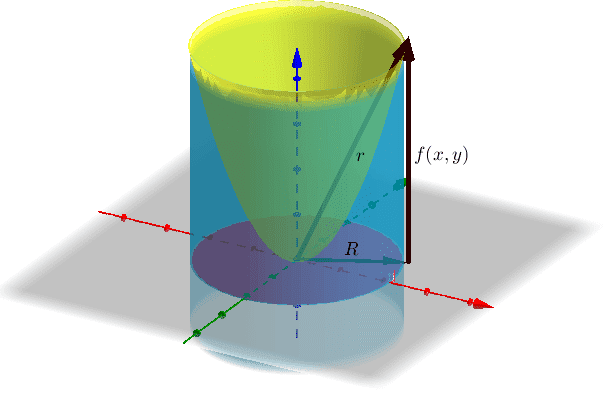
The field of a dipole distribution at a point $P$ is:

$\displaystyle\nabla\psi=-k \int_{V'} (\vec{\nabla'}.\vec{M'})\ \nabla \left( \dfrac{1}{r} \right) dV' +k \oint_{S'} (\vec{M'}.\hat{n}) \nabla \left( \dfrac{1}{r} \right) dS'$

If $P\in V'$ and $P\in S'$, the integrand is discontinuous (infinite) at the point $r=0$. If we use spherical and polar coordinates:

\begin{align}
\nabla\psi&=\bbox[orange,5px]{-k \int_{V'}
(\vec{\nabla'}.\vec{M'})\ \left( \dfrac{\hat{r}}{r^2} \right) r^2 \sin \theta\ d\theta\ d\phi\ dr}\\
&\bbox[pink,5px]{+ k \oint_{S'_1} (\vec{M'}.\hat{n}) \left( \dfrac{\hat{r}}{r} \right) \sqrt{{f_x}^2+{f_y}^2+1}\ \dfrac{R}{\sqrt{R^2+f^2}} dR\ d\theta'}
\bbox[yellow,5px] {+ k \oint_{S'_2}\dfrac{\vec{M'}.\hat{n}}{r}dS'}
\end{align}

The first term has the integrand continuous everywhere. The second term has the integrand discontinuous (infinite) at the point $r=0$.

(i) Is it necessary to remove a small circle around $R=0$ in order to remove the singularity in the second term so that we can compute the integral?

(ii) If so what about the contribution to the surface integral from the point $R=0$, i.e. $r=0$? Should we use Dirac delta here because the integrand is singular at $r=0$ and is the contribution to the surface integral from the point $r=0$ significant?

 

[fresh_42]

No, there are no removals and complicated considerations needed, just integrate it.

 

[Mike400]

No, there are no removals and complicated considerations needed, just integrate it.

But there is an $r^{-1}$ singularity (discontinuity) in the second term. How can we directly integrate it ? Shouldn't we need an improper integral?

 

[fresh_42]

It depends on whether we need this point in the antiderivative. We can integrate $\int \frac{1}{x}dx$, we just can't compute $\int_0^1 \frac{1}{x}dx$, i.e. it doesn't converge. You cannot remove this singularity with tricks.

 

[Mike400]

Does this mean that the electric field of a dipole distribution is not defined (or is divergent) at the surface of the distribution? And also in that case, the electric field should blow up near the surface. Wouldn't it be true then?

 

[fresh_42]

I moved this thread into our forum about Classical Physics, as this isn't a question about calculus anymore, but how to deal with possible singularities in physics. I'm no physicist, so I don't want to say something wrong here.

 

[Mike400]

Do you know of someone other in this site who can help?

 

[fresh_42]

I'm going to ask.

 

[Mike400]

I'm going to ask.

Thanks

 

[Charles Link]

If you take the surface integral, and change the point of origin about the singularity (by a transformation) the surface element is $dS=r \, dr d \theta$ , (in the plane of the surface that passes through the singularity), so that will in fact cancel the $r$ in the denominator. To see this with the algebraic form that you have for $dS'$ about an arbitrary origin is quite difficult.

 

[Mike400]

If you take the surface integral, and change the point of origin about the singularity (by a transformation) the surface element is $dS=r \, dr d \theta$ , (in the plane of the surface that passes through the singularity), so that will in fact cancel the $r$ in the denominator. To see this with the algebraic form that you have for $dS'$ about an arbitrary origin is quite difficult.

That's true for potential. But in the gradient of potential i.e. electric field we have $r^2$ in the denominator. One of them gets canceled out with $dS=r\ dr\ d\theta$ but the other remains.

 

[Charles Link]

That's true for potential. But in the gradient of potential i.e. electric field we have $r^2$ in the denominator. One of them gets canceled out with $dS=r\ dr\ d\theta$ but the other remains.

It (the surface integral) makes the potential $\psi=\psi(\vec{r})$ a well-behaved function of $\vec{r}$. To get the $\vec{H}$ you take the minus gradient of $\psi$, but you don't operate the gradient on the "primed" coordinates over which the integration is being performed. You need to operate the gradient on the $\vec{r}$ of $\psi(\vec{r})$.

 

[kimbyd]

That's true for potential. But in the gradient of potential i.e. electric field we have $r^2$ in the denominator. One of them gets canceled out with $dS=r\ dr\ d\theta$ but the other remains.

If I'm reading your calculations correctly, the gradient of the potential is integrated over the volume $dV$, which is $r^2 dr d\theta d\phi$, so it still cancels.

In principle you still should be careful about singularities which occur at any step in the calculation, even if they later cancel. But I think in this case it's well-behaved. It's possible to verify this by proving that cutting out an infinitessimal region around $r=0$ does not change the result. That is, if the radial part of the integral for $V'$ goes from $r = 0 \rightarrow r = r'$, then:
$$\lim_{r' \rightarrow 0} \psi(r') = 0$$

Verifying this is the case should be trivial to compute as you work through the calculations.

 

[Mike400]

If I'm reading your calculations correctly, the gradient of the potential is integrated over the volume $dV$, which is $r^2 dr d\theta d\phi$, so it still cancels.

In principle you still should be careful about singularities which occur at any step in the calculation, even if they later cancel. But I think in this case it's well-behaved. It's possible to verify this by proving that cutting out an infinitessimal region around $r=0$ does not change the result. That is, if the radial part of the integral for $V'$ goes from $r = 0 \rightarrow r = r'$, then:
$$\lim_{r' \rightarrow 0} \psi(r') = 0$$

Verifying this is the case should be trivial to compute as you work through the calculations.

That's right. Now what about the surface $\vec{H}$ singularity? Cutting out an infinitessimal region around $r=0$ doesn't make the integral converge. Shall we need to remove the surface singularity by other means if possible, or is $\vec{H}$ not defined (blows up) at the surface? What shall we do?

 

[kimbyd]

That's right. Now what about the surface $\vec{H}$ singularity? Cutting out an infinitessimal region around $r=0$ doesn't make the integral converge. Shall we need to remove the surface singularity by other means if possible, or is $\vec{H}$ not defined (blows up) at the surface? What shall we do?

I missed that. Why are you attempting to integrate over a surface which intersects with the point charge at $r=0$?

 

[Charles Link]

I missed that. Why are you attempting to integrate over a surface which intersects with the point charge at r=0r=0?

There is a finite "magnetic surface charge density" $\sigma_m=\vec{M} \cdot \hat{n}$ at $\vec{r}=0$, but there is no magnetic monopole there. $\\$
This is basically following the magnetic "pole" method (using $\rho_m=-\nabla \cdot \vec{M}$ and $\sigma_m=\vec{M} \cdot \hat{n}$ of computing the magnetic field $\vec{B}$ and using $\vec{B}=\mu_o \vec{H}+\vec{M}$ with $\vec{H}$ computed similarly to Coulomb's law, (with $\mu_o$ rather than $\epsilon_o$), rather than using bound magnetic currents, i.e. $\nabla \times \vec{M} =\mu_o \vec{J}_m$ and magnetic surface current density per unit length $\vec{K}_m=\vec{M} \times \hat{n}/\mu_o$ and Biot-Savart. $\\$ Here they are computing the $\vec{H} =-\nabla \psi$ in the absence of currents in conductors. $\\$ I think I covered it pretty well, but might you @vanhees71 have anything to add?

 

[Mike400]

I missed that. Why are you attempting to integrate over a surface which intersects with the point charge at $r=0$?

The magnetic charge here is that of a volume distribution having volume $V'$ and boundary $S'$. I am interested in knowing whether the $\vec{H}$ field exists (converges or diverges) at the boundary $S'$.

 

[kimbyd]

The magnetic charge here is that of a volume distribution having volume $V'$ and boundary $S'$. I am interested in knowing whether the $\vec{H}$ field exists (converges or diverges) at the boundary $S'$.

Ah, I see. Yes, that should be fine and it should be finite. I suspect the problem is as described by Charles Link in #12: the integral you're stating is divergent should be integrated over $r$ rather than $R$.

 

[Mike400]

It (the surface integral) makes the potential $\psi=\psi(\vec{r})$ a well-behaved function of $\vec{r}$. To get the $\vec{H}$ you take the minus gradient of $\psi$, but you don't operate the gradient on the "primed" coordinates over which the integration is being performed. You need to operate the gradient on the $\vec{r}$ of $\psi(\vec{r})$.

gradient on the "unprimed" coordinates

$\nabla. \dfrac{1}{|\vec{r}-\vec{r'}|}=-\dfrac{\vec{r}-\vec{r'}}{|\vec{r}-\vec{r'}|^3}$

gradient on the "primed" coordinates:

$\nabla'. \dfrac{1}{|\vec{r}-\vec{r'}|}=\dfrac{\vec{r}-\vec{r'}}{|\vec{r}-\vec{r'}|^3}$

There is only a difference in the sign.

Still $\vec{H}$ field diverges at the boundary

 

[Charles Link]

You could compare these magnetic charges to the analogous electrical problem. A finite charge density $\rho$ and finite surface charge density $\sigma$ does not cause $V$ or $\vec{E }$ to diverge. $V$ is continuous and $\vec{E}$ is always finite. $\\$ The same can not be said for a charge $Q$.
$\\$ In this problem, there are no magnetic monopoles $Q_M$. There is only magnetic charge density $\rho_m=-\nabla \cdot M$ and magnetic surface charge density $\sigma_m=\vec{M} \cdot \hat{n}$. The computations of $\vec{E}$ and $\vec{H}$ are completely analogous with one using $\epsilon_o$ and the other $\mu_o$.

 

[Mike400]

You could compare these magnetic charges to the analogous electrical problem. A finite charge density $\rho$ and finite surface charge density $\sigma$ does not cause $V$ or $\vec{E }$ to diverge. $V$ is continuous and $\vec{E}$ is always finite. $\\$ The same can not be said for a charge $Q$.
$\\$ In this problem, there are no magnetic monopoles $Q_M$. There is only magnetic charge density $\rho_m=-\nabla \cdot M$ and magnetic surface charge density $\sigma_m=\vec{M} \cdot \hat{n}$. The computations of $\vec{E}$ and $\vec{H}$ are completely analogous with one using $\epsilon_o$ and the other $\mu_o$.

Yes, they are analogous. I have asked a similar question from electrostatic viewpoint here.

 

[Charles Link]

Yes, they are analogous. I have asked a similar question from electrostatic viewpoint here.

Perhaps someone can very patiently show you why these integrals with finite $\rho$ and finite $\sigma$ do not diverge, but I think you really need to work it out for yourself. I have given it my best effort, but it has been very difficult to convince you of this.

 

[Mike400]

Perhaps someone can very patiently show you why these integrals with finite $\rho$ and finite $\sigma$ do not diverge, but I think you really need to work it out for yourself. I have given it my best effort, but it has been very difficult to convince you of this.

I have been on this problem for almost a month. Can you please try a little more on explaining why they do not diverge. Or please give a hint about the key secret behind their convergence. Also please have a look at #4.

 

[Charles Link]

When computing the potential for a finite surface charge density across an infinite plane, $E =\frac{\sigma}{2 \epsilon_o}$, and the potential doesn't change at all in going through the surface charge density layer from right to left or left to right. Trying to prove this mathematically for the general case using $V$ and $\vec{E }$ might be somewhat difficult.
$\\$ Similar results apply with a charge density $\rho$. The field at the center of a sphere of charge density $\rho$ is zero. There is no additional contribution to $V$ as the center of the charged sphere with charge density $\rho$ is approached . By Gauss' law, $\vec{E}=0$ at the center. $\\$ $\frac{4 \pi R^3}{3} \frac{\rho}{\epsilon_o}=4 \pi R^2 E$. This means $E=0$ as $R \rightarrow 0$.
The general case is much harder to compute.

 

[Charles Link]

You might consider the general case to be composed of super-positions of a couple of basic building blocks. Perhaps that would complete the proof.
Even near the surface of a small disc of surface charge density $\sigma$, we find $E=\frac{\sigma}{2 \epsilon_o}$. The electric field does not experience a singularity here.

 

[kimbyd]

gradient on the "unprimed" coordinates

$\nabla. \dfrac{1}{|\vec{r}-\vec{r'}|}=-\dfrac{\vec{r}-\vec{r'}}{|\vec{r}-\vec{r'}|^3}$

gradient on the "primed" coordinates:

$\nabla'. \dfrac{1}{|\vec{r}-\vec{r'}|}=\dfrac{\vec{r}-\vec{r'}}{|\vec{r}-\vec{r'}|^3}$

There is only a difference in the sign.

Still $\vec{H}$ field diverges at the boundary

You stated that the following integral diverges:
$${k \oint_{S'_1} (\vec{M'}.\hat{n}) \left( \dfrac{\hat{r}}{r} \right) \sqrt{{f_x}^2+{f_y}^2+1}\ \dfrac{R}{\sqrt{R^2+f^2}} dR\ d\theta'}$$
This doesn't diverge if you replace $R$ with $r$, provided $f > 0$.

I don't think you ever defined $f$ in your post, however. Could you please elaborate on what this is, and what $f_x$ and $f_y$ are?

 

[Charles Link]

@kimbyd I think I can answer your question, which the OP has a diagram for in post 1.
Given the surface, $z=f(x,y)$ or $F(x,y,z)=f(x,y)-z=0$.
We have that $\nabla F$ is normal to the surface. $\\$ For these surface integrals we need to find $\sec{\gamma}=\frac{1}{\cos{\gamma}}$ where $\cos{\gamma}=\hat{k} \cdot \frac{\nabla F}{|\nabla F|}$.
Now $\nabla F=F_x \hat{i}+F_y \hat{j}-\hat{k}$.
This means $\sec{\gamma}=- \sqrt{F_x^2+F_y^2+1}$ with the minus sign really being irrelevant.
Here $F_x=\frac{\partial{F}}{\partial{x}}$ and $F_y=\frac{\partial{F}}{\partial{y}}$.

 

[Charles Link]

I am a little puzzled by the diagram of post 1. The region where $\vec{M}$ is non-zero is presumably the region below the paraboloid, and you want to find the contribution to the integral at a point $\vec{r}$ that lies on the paraboloid. The integral over $R$ is ok, but the $\vec{r}$ in the diagram needs to be $\vec{r}'$, and the $r$ in the denominator is $r=|\vec{r}-\vec{r}'|$. This $r$ is really a poor choice of letters, and perhaps should be called letter $s$ . It's very clumsy to work with these complicated surface integral formulas and prove anything meaningful. It's much easier to simplify what's going on, and to prove things for the simplified case.

 

[Mike400]

I am a little puzzled by the diagram of post 1. The region where $M$ is non-zero is presumably the region below the paraboloid, and you want to find the contribution to the integral at a point $\vec{r}$ that lies on the paraboloid. The integral over $R$ is ok, but the $\vec{r}$ in the diagram needs to be $\vec{r}'$, and the $r$ in the denominator is $r= |\vec{r}-\vec{r}' |$. This $r$ is really a poor choice of letters, and perhaps should be called letter $s$.

I see. You are correct.

 

[Mike400]

You stated that the following integral diverges:
$${k \oint_{S'_1} (\vec{M'}.\hat{n}) \left( \dfrac{\hat{r}}{r} \right) \sqrt{{f_x}^2+{f_y}^2+1}\ \dfrac{R}{\sqrt{R^2+f^2}} dR\ d\theta'}$$
This doesn't diverge if you replace $R$ with $r$, provided $f > 0$.

I don't think you ever defined $f$ in your post, however. Could you please elaborate on what this is, and what $f_x$ and $f_y$ are?

Charles Link has given a convincing answer.

I had earlier looked into this problem from a different point of view. I needed to compute the integral at a point $P∈S′$.

$\displaystyle k \oint_{S'} (\vec{M'}.\hat{n}) \nabla \left( \dfrac{1}{r} \right) dS' =-k \oint_{S'} (\vec{M'}.\hat{n}) \dfrac{\hat{r}}{r^2} dS'$

I took the origin of my Cartesian coordinate system at $P$ and took the $x$-$y$ plane as the plane which is tangent to the surface $S′$ at point $P$. Then I divided my domain into two parts: One containing the surface $S′_1$ whose projection in $x-y$ plane is a circle $A$ around point $P$. The other the rest of the surface $S′_2$.

As there are no singular points in $S′_2$, its contribution to the surface integral is finite.

As for $S′_1$ which contains a singular point at origin $P$, I changed my domain from $S′_1$ to $A$. In doing so, I had to introduce the function $z=f(x,y)$ which is a function dependent on the shape of $S′_1$. Thus $dS′$ was replaced with $\sqrt{f_x^2+f_y^2+1} dA′=\sqrt{f_x^2+f_y^2+1} R′ dR′ dθ'$ where $f_x$ and $f_y$ are partial derivatives of $f(x,y)$ w.r.t. $x$ and $y$ respectively.

Also, I replaced $r'$ with $\sqrt{R^2+f^2}$

I now understand why field is finite at the surface. However I still do not understand why this approach fails to converge.