Direction cosine matrix of rolling disk on circular ring

[QuantumLollipop]

Hey all,
I'm stuck on this problem and not sure how to proceed/if I'm in the right direction.

Problem: One reference frame N sits at the origin (inertial frame) while another frame, B, describes a disk rolling on a circular ring about the other frame. Picture below

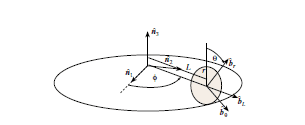(A) find the direction cosine matrix [BN] in terms of angle phi
(B) Given a vector in the B frame find the vector in the N frame

Relevant Equations: The direction cosine matrix of a homogeneous system such as this is a 4x4 matrix whose elements are: top left ([BN], rotation matrix as if centered at origin)3x3, top right (a vector from the origin of N frame to origin of B frame)3x1, bottom left (0)1x3, bottom right (1)1x1 = [NB]4x4

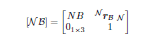Attempt:
The position vector was relatively easy to compute:
r(N)=L*cos(Φ) n1^{^} + L*sin(Φ) n2^{^} + r n3^{^} (I hope that's right)

Next, to complete the full matrix I need to find the direction cosine matrix NB which I believe is computed as if B were sitting at the origin.

I'm having difficulty with this part, I assume the only way to find this is using the 3 consecutive Euler Angles. My trouble is finding which Euler Angles to use for the rotation. Any help would be appreciated. Apologies for the crude equations, I was having troubles with the equation editor and couldn't figure out how to make matrices. Thanks

 

[felmon38]

The problem can be modelling as the figure, where there are three rigid solids or reference systems: 0 is the laboratory, 1 is an auxiliary solid which rotates about the vertical axe z with respect to 0, this rotation is modelling as a motor of rotation its axis is fixed to 0 and, finally, 2 is the disk which rotate with respect to 1 . This movement is modelling as a motor which housing is fixed to the before motor housing, and its shaft is fixed to the disk. I'm using the same formulation as used in the the robotic field.
At the initial position, origin of the rotation angles, the three coordinates systems of the three solids are coincidentes.
After this, is easy to find the matrixes B_ij,(3x3) base change, as the T_ij (4x4) coordinate change matrix

B₁₀=[[Cφ,-Sφ,0],[Sφ,Cφ,0],[0,0,1]]
B₂₁=[[Cθ,0,Sθ],[0,1,0],[-Sθ,0,Cθ]]
B₂₀=B₁₀.B₂₁T₁₀=[[Cφ,-Sφ,0,0],[Sφ,Cφ,0,0],[0,0,1,0],[0,0,0,1]]
T₂₁=[[Cθ,0,Sθ,0],[0,1,0,0],[-Sθ,0,Cθ,0],[0,0,0,1]]
T₂₀=T₁₀.T₂₁
According to your fig.; L.φ=-r.θ

(A) B₂₀
(B) {r}₀=B₂₀.{r}₂

I hope you can understand my bad english. Sorry.