ddcz
- 1
- 0
This question pertains to the classic ladder-leaning-against frictionless wall scenario. The system is in static equilibrium. The ladder is thin and can be assumed to be made of a homogeneous material so that the center-of-mass lies at the geometric center.
The forces in this scenario is well-known, and diagrammed as follows. This type of problem can be solved by equating the sum of forces and torques to zero at any and all points, as is commonly done in static equilibrium problems.
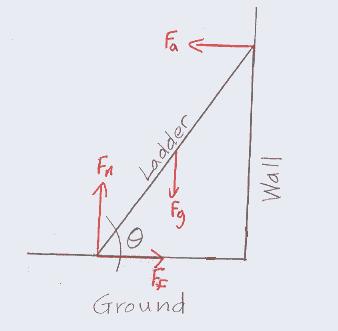
My question is: Is the direction of the force exerted by the ground on the ladder aligned with the ladder itself? That is, is the force exerted by the ground on the ladder in the direction \theta, as shown in the diagram?
This hypothesis seems plausible to me, because as theta becomes large (ladder is almost vertical), the force in question is also almost at 90 degrees. As theta approaches zero (ladder is almost horizontal), there is a large horizontal component, so the force is almost horizontal (to the right).
Could anyone confirm or disprove my hypothesis?
The forces in this scenario is well-known, and diagrammed as follows. This type of problem can be solved by equating the sum of forces and torques to zero at any and all points, as is commonly done in static equilibrium problems.
My question is: Is the direction of the force exerted by the ground on the ladder aligned with the ladder itself? That is, is the force exerted by the ground on the ladder in the direction \theta, as shown in the diagram?
This hypothesis seems plausible to me, because as theta becomes large (ladder is almost vertical), the force in question is also almost at 90 degrees. As theta approaches zero (ladder is almost horizontal), there is a large horizontal component, so the force is almost horizontal (to the right).
Could anyone confirm or disprove my hypothesis?