Direction of friction acting on a rolling object

[Alettix]

Hi!

My question considers no specific problem, but rather different concepts I have trouble getting my head around. So I would be really happy if you could help me understand different kinds of friction, and maybe above all their direction, acting on a rolling object. :)

Fist we have kinetic fricition acting on an object which is slipping while rolling. This one points in the direction of propagation, thus exerting a negativ torque and slowing the rotation down until rolling without slipping is estabilished. Am I right?

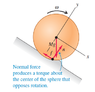
Then there is the rolling friction caused by the surface of the object and ground being not perfectly rigid, resulting in the normal force exerting a negative torque. But can we in this case define any direction of friction?

What I then find really confusing is, for instance, problems dealing with tires moving or accelerating upwars on an inclined plane. In this case (in those problems I have solved), the friction is always pointing upwards along the plane. What kind of friction is this? I can understand that this force can accelerate the tire upwards if we treat it as a point object, but looking at it as on a rigid body, it seems like this force should extert a negativ torque and slow the rotation down! But in that case the tire could not roll up on the plane... So where does my reasoning fail? Why doesn't the fricition slow the rotation down?

An other kind of problem which confuses me is the one where an object starts from rest and is then made to rotate and roll by a friction force, this time directed in the opposite direction, that's in the opposite direction of propagation. What kind of friction is this? And how is the friction directed when an object is simply rolling on a surface without any inclination and why?

Many Thanks! :)

 

[mooncrater]

I have got this line from a link , I think it may give you an idea-
" Friction always opposes relative motion of the point of contact . To know the direction of friction assume that no friction is present and see the direction in which point of contact is moving :friction is opposite to that direction."

 

[Redbelly98]

What I then find really confusing is, for instance, problems dealing with tires moving or accelerating upwars on an inclined plane. In this case (in those problems I have solved), the friction is always pointing upwards along the plane. What kind of friction is this? I can understand that this force can accelerate the tire upwards if we treat it as a point object, but looking at it as on a rigid body, it seems like this force should extert a negativ torque and slow the rotation down! But in that case the tire could not roll up on the plane... So where does my reasoning fail? Why doesn't the fricition slow the rotation down?

This is static friction. It does act upward along the ramp, *and* it slows the rotation down -- for a (unpowered) tire or wheel rolling up the ramp.

Let's say the ramp surface goes up and to the right (like the "/" character), and that the wheel is rolling upward -- so the wheel is turning clockwise. We know that the wheel slows down and eventually comes to a momentary stop somewhere up the ramp, so the torque from friction must be counterclockwise -- opposite the direction of rotation -- about the wheel's center of mass. This means the friction points up and to the right at the contact point.

Oddly, this means that friction acts to propel the wheel farther than it would go than if there were no friction -- compared to say a block sliding up a frictionless ramp. But that is just what it does.

An other kind of problem which confuses me is the one where an object starts from rest and is then made to rotate and roll by a friction force, this time directed in the opposite direction, that's in the opposite direction of propagation. What kind of friction is this?

I don't follow what you are describing here. I'm not aware of friction being able to start a resting object moving.

And how is the friction directed when an object is simply rolling on a surface without any inclination and why?

If it's a level surface, static friction does nothing, but rolling friction will slow the object down.

 

[A.T.]

My question considers no specific problem, but rather different concepts I have trouble getting my head around. So I would be really happy if you could help me understand different kinds of friction, and maybe above all their direction, acting on a rolling object. :)

- Rolling resistance due to deformation always opposes the current movement of the whole wheel.

- Sliding friction always opposes the local relative motion of the contact patches.

- Static friction during acceleration depends on how much net linear force vs. torque you apply to propel/brake the wheel. Depending on the mass vs. moment of inertia there are combinations of applied linear force and torque that result in zero static friction during acceleration. Deviating from that ratio one way or the other will result in static friction pointing one way or the other.

 

[Alettix]

I have got this line from a link , I think it may give you an idea-
" Friction always opposes relative motion of the point of contact . To know the direction of friction assume that no friction is present and see the direction in which point of contact is moving :friction is opposite to that direction."

Thank you, this helps with the kinetic friction. :)

 

[Tom_K]

You may find this paper helpful.

 

[Alettix]

Firstly, Thank you for your answer! :)

This is static friction. It does act upward along the ramp, *and* it slows the rotation down -- for a (unpowered) tire or wheel rolling up the ramp.

So this means that in order to accelerate upwards we must have another force (besides weight, friction and normal) acting on the tire so the net-torque is in the clockwise direction (if the ramp is like "/")?

Let's say the ramp surface goes up and to the right (like the "/" character), and that the wheel is rolling upward -- so the wheel is turning clockwise. We know that the wheel slows down and eventually comes to a momentary stop somewhere up the ramp, so the torque from friction must be counterclockwise -- opposite the direction of rotation -- about the wheel's center of mass. This means the friction points up and to the right at the contact point.

Oddly, this means that friction acts to propel the wheel farther than it would go than if there were no friction -- compared to say a block sliding up a frictionless ramp. But that is just what it does.

This is what confuses me... Did you come to this conclusion by treating the wheel as a pointmass?

I don't follow what you are describing here. I'm not aware of friction being able to start a resting object moving.

My apologies for the bad despcription. This problem comes from the international physics olympiad 2014, where one had to calculate the force acting on a small pointmass when rolling inside a hollow, thin walled cylinder with radius R. The whole system started from rest and the point mass was on a height of R (on the core of the cylinder). Then when the small mass was released, the cylinder started rolling. I saw a teacher solving the problem, and in his freebody diagram the friction pointed in the opposite direction of propagation, thus giving the cylinder a torque and starting it from rest. I can understand that the friction has to have this direction in order to the cylinder being able to start rolling, but I don't know what kind of friction this is, nor if it will change direction if the cylinder reaches constant velocity.

If it's a level surface, static friction does nothing, but rolling friction will slow the object down.

I just took another look in my textbook (University Physics by Young and Freedman) and noticed something about rolling friction which confuses me. In a picture, the normal force is dirceted upwards (but not going through the center of mass) thus leading to a torque which slows the rotation down. However, in the picture there is also a kinetic frictionforce directed opposite the direction of propagation, in that way giving a positiv torque. Now, the coefficient of friction is usually smaller than unity, so the friction force will not be as great as the normalforce. But at the same time, the lever arm of the frictionforce is much greater than that of the normalforce!
Of course I understand that the object can not start accelerating all by it self, as this would violate energyconservation, but still how comes we can't have a net positive torque?

Thank you! :)

 

[Alettix]

- Static friction during acceleration depends on how much net linear force vs. torque you apply to propel/brake the wheel. Depending on the mass vs. moment of inertia there are combinations of applied linear force and torque that result in zero static friction during acceleration. Deviating from that ratio one way or the other will result in static friction pointing one way or the other.

Thank you!
Hm, I have never encountered a problem where the static friction is pointed downwards for a wheel accelerating upwards, nor one where there is zero static friction. Do you have any example of it or know where I can find one? :)

 

[Alettix]

You may find this paper helpful.

Thank you!

 

[A.T.]

Thank you, this helps with the kinetic friction. :)

For static friction this part of the quote is relevant "assume that no friction is present and see the direction in which point of contact is moving :friction is opposite to that direction." Which basically boils down to what I wrote about considering all the other forces & torques on the wheel.

Maybe you can put it this way:

- Kinetic friction tries to achieve clean rolling, by opposing the mismatch of:

linear velocity vs. angular velocity * radius.

- Static friction tries to sustain clean rolling, by providing the force & torque needed to keep:

linear acceleration = angular acceleration * radius.

Hm, I have never encountered a problem where the static friction is pointed downwards for a wheel accelerating upwards, nor one where there is zero static friction.

If you accelerate the wheel up an incline by applying a linear force at the axle, the static friction will have to provide the angular acceleration and will point down the incline. If additionally to the linear force you also provide an appropriate torque for the angular acceleration, no static friction is needed.

 

[Alettix]

Thank you so much A.T!
I will try to digest this, but I think I have finally started to get my head around it. :)

 

[Redbelly98]

Firstly, Thank you for your answer! :)

This is static friction. It does act upward along the ramp, *and* it slows the rotation down -- for a (unpowered) tire or wheel rolling up the ramp.

So this means that in order to accelerate upwards we must have another force (besides weight, friction and normal) acting on the tire so the net-torque is in the clockwise direction (if the ramp is like "/")?

Yes.

Let's say the ramp surface goes up and to the right (like the "/" character), and that the wheel is rolling upward -- so the wheel is turning clockwise. We know that the wheel slows down and eventually comes to a momentary stop somewhere up the ramp, so the torque from friction must be counterclockwise -- opposite the direction of rotation -- about the wheel's center of mass. This means the friction points up and to the right at the contact point.

Oddly, this means that friction acts to propel the wheel farther than it would go than if there were no friction -- compared to say a block sliding up a frictionless ramp. But that is just what it does.

This is what confuses me... Did you come to this conclusion by treating the wheel as a pointmass?

No, I am treating it as a regular wheel. And applying the rotational version of Newton's 2nd law about the wheel's center of mass:

Net torque = (rotational inertia) x (angular acceleration)

A counterclockwise angular acceleration means there is a counterclockwise net torque about the wheel's center of mass. But the normal force and gravitation forces are directed through the center of mass ... so that leaves only 1 force that is responsible for the torque.

I don't follow what you are describing here. I'm not aware of friction being able to start a resting object moving.

My apologies for the bad despcription. This problem comes from the international physics olympiad 2014, where one had to calculate the force acting on a small pointmass when rolling inside a hollow, thin walled cylinder with radius R. The whole system started from rest and the point mass was on a height of R (on the core of the cylinder). Then when the small mass was released, the cylinder started rolling. I saw a teacher solving the problem, and in his freebody diagram the friction pointed in the opposite direction of propagation, thus giving the cylinder a torque and starting it from rest. I can understand that the friction has to have this direction in order to the cylinder being able to start rolling, but I don't know what kind of friction this is, nor if it will change direction if the cylinder reaches constant velocity.

Well, rolling friction rarely comes up in physics problems like this. Not saying that it never does, but it would very surprising if it did. So just think about what the surfaces are doing: if they are slipping by one another, it's kinetic friction. If the surfaces do not slip, then it's static friction.

I just took another look in my textbook (University Physics by Young and Freedman) and noticed something about rolling friction which confuses me. In a picture, the normal force is dirceted upwards (but not going through the center of mass) thus leading to a torque which slows the rotation down. However, in the picture there is also a kinetic frictionforce directed opposite the direction of propagation, in that way giving a positiv torque. Now, the coefficient of friction is usually smaller than unity, so the friction force will not be as great as the normalforce. But at the same time, the lever arm of the frictionforce is much greater than that of the normalforce!
Of course I understand that the object can not start accelerating all by it self, as this would violate energyconservation, but still how comes we can't have a net positive torque?

Thank you! :)

I guess I'd have to see Young & Freedman's picture to give a good answer.

 

[Alettix]

Thank you once again! :)

I guess I'd have to see Young & Freedman's picture to give a good answer.

I included it!