Discrete Mathematics : Proof : Question 1

[Supierreious]

Homework Statement

Question 1 :

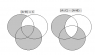
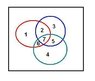
a) Use Venn diagrams to determine whether or not, for all subnets A,B and C of a universal set U, (A-B) ∪ C = (A∪C) - (A∩B)
b) If the statement appears to hold, give a proof, if not, give a counter example.

Homework Equations

(A-B) ∪ C = (A∪C) - (A∩B)

*there are no other variables given
*no other values are known
*this question relates to the proof

The Attempt at a Solution

a) I have drawn the Venn diagrams, which does not reflect that they equate to each other, so they are not equal.
b) The counter example is the one I am struggling with, so i will explain how i did it, and basically just adapted an answer from my textbook :

Attempt to prove with counter example :
------------------------------------------------------------

Let : A = {1;2}
Let : B = {2;3}
Let : C = {1;4}

Left hand : (A-B) ∪ C :

(A-B) = = {1;2} - {2;3} = {1;3}
(A-B) ∪ C = {1;3} ∪ C = {1;3} ∪ {1;4} = {1;3;4}

(A-B) ∪ C = {1;3;4}

Now to find out what the right hand side is :

(A∪C) - (A∩B) :

(A∪C) = {1;2}∪{1;4} = {1;2;4}
(A∩B) = {1;2}∩{2;3} = {2}
(A∪C) - (A∩B) = {1;4}



Thus :

(A-B) ∪ C ≠ (A∪C) - (A∩B)


-----------------------------------------------------------------------------

Please let me know if this is right, or where i can improve, this is something new to me, and i still need to work on this a lot.

 

[who_]

Your steps are not correct. A - B is the difference, so
A - B = {1,2} - {2,3} = {1}. You are removing elements in AnB from A.

So, what you have is not a counter example. Try again :)

 

[who_]

Your steps are not correct. A - B is the difference, so
A - B = {1,2} - {2,3} = {1}. You are removing elements in AnB from A.

So, what you have is not a counter example. Try again :)

 

[Supierreious]

Thanks,

=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;
Left hand : (A-B) ∪ C :

(A-B) = = {1;2} - {2;3} = {1;3}
(A-B) ∪ C = {1;3} ∪ C = {1;3} ∪ {1;4} = {1;3;4}

(A-B) ∪ C = {1;3;4}
=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;

should be :

=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;=;

Left hand : (A-B) ∪ C :

(A-B) = = {1;2} - {2;3} = {1}
(A-B) ∪ C = {1} ∪ C = {1} ∪ {1;4} = {1;4}

(A-B) ∪ C = {1;4}

...

So that means that they are in fact the same... (i did not see that from my Venn diagram).

I will quickly draw the venn diagrams again, is there a way i can show you the venn diagrams on this forum ?

 

[Supierreious]

Ok, i have managed to upload a Venn diagram on these 2.

Please let me know why my venn diagram does not reflect the calculation..

 

[ehild]

Ingenious! Your Venn diagrams are correct. If you find 3 sets which obey the original statement it can be still false. Find a counter-example. What about the sets in the attachment?

ehild

 

[who_]

Yes - if A n B n C is not empty, the proposition is false.

 

[Supierreious]

hi Ehild,

Thank you for the feedback, yes i can see the difference, only if a place a value in every field :)

The example i used had 'empty fields' - which does not point out the difference.

So in the process of answering this one (Correct me if i am wrong) :

1. Draw the venn diagrams
2. Put a value in every section (piece) of the venn diagram
3. Then do the calculations - due to the fields of the venn diagram , when writing out the proof it will be clear that the two are not the same

Just writing out my proof, if you can confirm, i will really appreciate it :


A = {1;2;6;7}
B = {2;3;5;7}
C = {4;5;6;7}

(A-B) ∪ C = {1;2;6;7} - {2;3;5;7} ∪ C
= {1;6} ∪ C
= {1;6} ∪ {4;5;6;7}
= {1;4;5;6;7}

Right Hand : ∪ ∩

(A∪C) - (A∩ B)
(A∪C) : {1;2;6;7) ∪ {4;5;6;7} = {1;2;4;5;6;7}
(A∩B) : {1;2;6;7} ∩ {2;3;5;7} = {2;7}
(A∪C) - (A∩ B) = {1;4;5;6}

and Thus :

(A-B) ∪ C ≠ (A∪C) - (A∩B)

 

[who_]

Nice, that works. A simpler example might have been:
A = B = C = {1}.

:)

 

[Supierreious]

Who, Ehild,

thanks a lot for your assistance, appreciated!