Disk falling while rotating round a point

[Karol]

Homework Statement

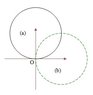
The disk of mass m and radius R is at position (a), upwards. it is free to rotate round point O on it's circumference.
If falls and reaches state (b), horizontal position.
What are the velocities and accelerations in position (b)

Homework Equations

Moment of inertia of a disk: $I=\frac{1}{2}mR^2$
Torque of rigid body: $M=I\alpha$
Energy of a rigid body: $E=\frac{1}{2}I\omega^2$
Centripetal acceleration: $a_{cen}=\frac{v^2}{R}=\omega^2 R$

The Attempt at a Solution

The angular velocity ω is from energy conservation:
$$mgR=mR^2\left( \frac{1}{2}+1 \right)\omega^2\; \rightarrow \omega^2=\frac{4g}{3R}$$
COM's velocity is $v_{cm}=\omega R=\sqrt{\frac{4g}{3R}}R=2\sqrt{\frac{gR}{3}}$
The radial velocity from the circular motion:
$$a_{cen}=\omega^2 R=\frac{4g}{3}$$
Tangential acceleration is from the gravity:
$$M=I\alpha\rightarrow mgR=\frac{3}{2}mR^2\alpha\rightarrow\alpha=\frac{2g}{3R}$$
$$a_{tan}=R\alpha=\frac{2g}{3}$$

 

[mfb]

Looks right.

 

[haruspex]

One typo... where you wrote radial velocity you meant radial acceleration.

 

[Karol]

Thanks