Dispersion relation for the free electron model

[Crosshash]

I'm trying to get my head around what this means exactly. I've plotted the graph to help verse me with the functions that I've derived.

From the free electron model, the wavefunctions are treated as planewaves of the form

\psi_\mathbf{k}(\mathbf{r}) = e^{i\mathbf{k}\cdot\mathbf{r}}

Due to the lattice being periodic, the wavefunction needs to be periodic and this occurs for values of k_{x,y,z} which are of the form

<br /> k_{x,y,z} = \frac{2n\pi}{a}<br />

When you solve the Schrödinger equation with this wavefunction, the energy eigenvalues are of the form

E = \frac{\hbar^2 k^2}{2m}

which I've plotted as a dispersion relation to give:

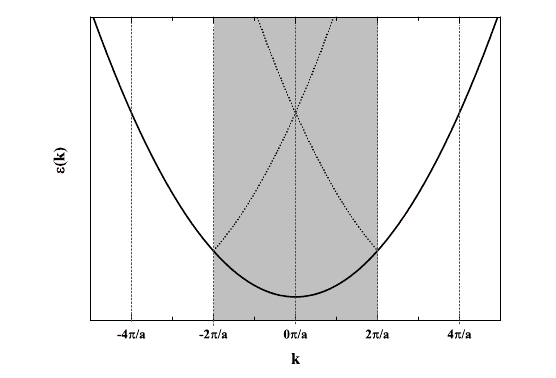
Here's where I'm trying to wrap my head around this. What exactly are we looking at here? Obviously, this is in reciprocal space. n is the quantum number but is it also the brillouin zone index? For n=1, two electrons can occupy that band, does that mean they're restricted to the first brillouin zone? For n=2, are they restricted to the second brillouin zone? Why do so many texts plot the dotted lines the way I've done it (inside the first brillouin zone). What consequence is this?

Thank you

[edit] just to add, I'm working through chapter 6 of Kittel.

 

[DrDu]

It's another way of classifying the wavefunctions. The wavefunctions corresponding to the dotted lines have one or more nodes inside every elementary cell (at least their real and imaginary part individually). So you can label the wavefunctions instead of the value of k, by $k \mod 2\pi/a$ and the number of nodes n. This characterization will be possible also when the electrons are not free.