Displacement Electric Field Outside Dielectric Material

[RyanUSF]

Homework Statement

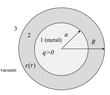
You have a conducting sphere (Region 1) of radius a carrying free charge q > 0 surrounded by a neutral dielectric shell (Region 2) of relative permittivity ε(r) = α/r, r ≥ R, where α is a constant with dimension of length, and vacuum outside (Region 3).

Find Displacement field everywhere.

Relevant Equations

D = ε_0*ε(r)*E
Where ε_0 is permittivity of free space, and ε(r) is the relative permittivity, and E is the electric field.

I know that inside region 1, the D-field is zero as it is a conducting sphere, the E-field must be zero. It makes sense that in region 2 (inside the dielectric) there is a D-field.

My question is, is there a D-field outside the dielectric material (r>R)? Obviously there will be an E-field, but now there is only the permittivity of free space, ε(r) is 0 correct? So is the D-field zero outside dielectric material or is it continuous?

 

[hutchphd]

The equation you quote is good everywhere. What does it tell you? What you say about $\epsilon (r)$ is incorrect. It is 1

 

[RyanUSF]

So with that being said, the D field outside (region 3) essentially becomes the what the electric field would be in that region (multiplied by ε_0 of course). D (r>R) = q/(4*pi*r^2), units of C/m^2 look good.

 

[hutchphd]

Also do you understand the continuity question? There are bound (polarization) charges and free charges, and you need to understand which is important for D and for E so tell me about it.

 

[RyanUSF]

The continuity equation states that the change in bound charge density with respect to time will equal the negative value of the divergence of bound current density.

For this problem it is a static case so it makes sense, change in charge density is 0 and there is no current density.

The bound charge density will relate to the polarization.

 

[hutchphd]

The continuity equation states that the change in bound charge density with respect to time will equal the negative value of the divergence of bound current density.

True but not complete.
Is the E field contiuous across the inner (r=a) surface)? By how much does it change?

 

[RyanUSF]

True but not complete.
Is the E field contiuous across the inner (r=a) surface)? By how much does it change?

For r<a the electric field must be 0. At r=a there is a surface charge over the sphere giving an E(r=a)=q/4*pi*ε_0*a^2. a<r<R E will change by dividing by ε(r).