Displacement Vectors finding magnitude of R and theta

[mariner962]

Homework Statement

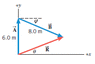
The displacement vectors A and B, when added together, give the resultant vector R, so that R= A+B . Use the data in the drawing and the fact that = 29° to find the magnitude R of the resultant vector and the angle θ that it makes with the +x axis.

I am unsure how to find the magnitude of R and theta

 

[Modulated]

Any ideas where to start?

 

[mariner962]

I know that the angle of 151 degrees is opposite the resultant and that i can use the law of cosines.

 

[mariner962]

actually i know that i have to find that angle using cosines