mariner962
- 6
- 0
Homework Statement
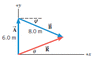
The displacement vectors A and B, when added together, give the resultant vector R, so that R= A+B . Use the data in the drawing and the fact that = 29° to find the magnitude R of the resultant vector and the angle θ that it makes with the +x axis.
I am unsure how to find the magnitude of R and theta