Distance between two cities on earth

[vizakenjack]

Assume that the Earth is spherical and recall that latitudes range from 0° at the Equator to 90° N at the North Pole. Consider Dubuque, Iowa (42.50° N latitude), and Guatemala City (14.62° N latitude). The two cities lie on approximately the same longitude. Do not neglect the curvature of the Earth in determining the following.
(c)

Here's the visual representation of the problem:

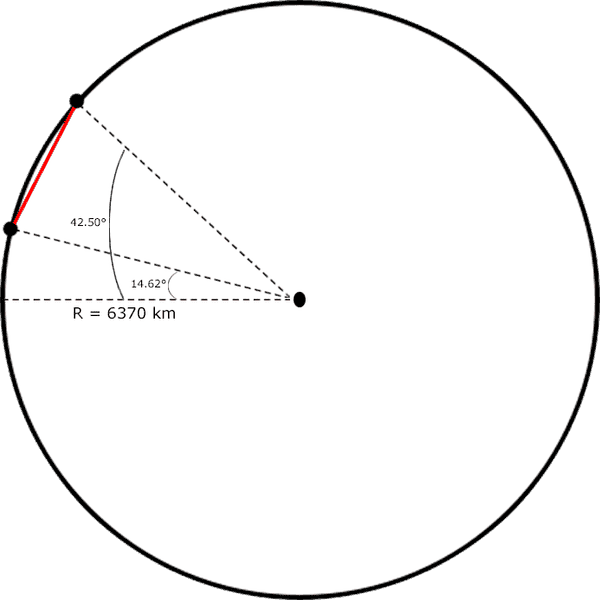For simplicity sake, we take a look at the Earth when the two cities are about to disappear from our field of view, so they kinda lie on the left edge of the earth... (I don't know how to say it better).

Anyhow,
I need to find the length of the red line, right?

I know what the correct formulas are:
R * (ΔΘ * pi/180), in other words radius times the difference between the angles in radians.

2nd formula to finding the answer is:
2 * R * sin(ΔΘ/2)

I kinda get the second formula, but why is the 1st formula correct?
Doesn't it find the arc length? Since ΔΘ is converted to radians?

Or did I draw the positions of the two cities incorrectly? Should the second city, Guatemala, be located exactly below Dubuque? But in that case, they would have different length from the center of the circle. So I really doubt they should be drawn in the same vertical axis.Let's plug in some values into the 2nd formula.
ΔΘ = 42.50°- 14.62° = 27.88° is the angle of a formed isosceles triangle with the red line as the base.
However, we don't need the whole angle of this newly formed triangle because it's easier to divide the triangle into two parts, and then find the missing side (x/2).

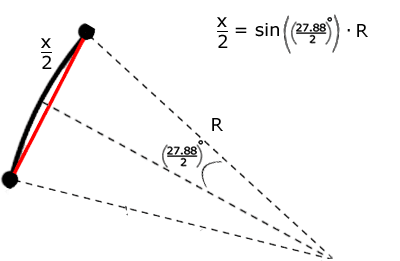in which case, x = sin(27.88°/2) * R * 2

 

[Orodruin]

The formulas are not equivalent. One of them computes the length of the red line and the other the length along the Earth's surface. Which one to use depends on what is actually being asked for.

 

[vela]

The fact that the problem statement says not to neglect the curvature of the Earth suggests which formula is the correct one to use. Which one do you think it is?

 

[vizakenjack]

The formulas are not equivalent. One of them computes the length of the red line and the other the length along the Earth's surface. Which one to use depends on what is actually being asked for.

So, like I said,

I kinda get the second formula, but why is the 1st formula correct?
Doesn't it find the arc length? Since ΔΘ is converted to radians?

first formula yields the arc length.

The fact that the problem statement says not to neglect the curvature of the Earth suggests which formula is the correct one to use. Which one do you think it is?

2nd one.

 

[NTW]

It's very easy... Both cities are approximately on the same meridian, and the difference in latitude is 42.50º - 14.62º = 27.88º.

Now, 360º along the meridian will be 6370 km × 2π = 40024 km.

Calculating the proportion 27.88º/360º, the answer is...

 

[vizakenjack]

It's very easy... Both cities are approximately on the same meridian, and the difference in latitude is 42.50º - 14.62º = 27.88º.

Now, 360º along the meridian will be 6370 km × 2π = 40024 km.

Calculating the proportion 27.88º/360º, the answer is...

So the proportions are: 27.88/360 = x/40024km
x = 3099.64 km
But the answer given by the 2nd formula yields 3069 km. Which formula yields a more precise answer?

 

[SammyS]

2nd one.

No. The second one does neglect curvature !

 

[vizakenjack]

No. The second one does neglect curvature !

Why couldn't anyone just simply say that an arc length is needed to be found.

So I'm guessing, in my triangle drawing, the red line isn't what I needed to find, right?
That means the answer given here was incorrect, no?

 

[Orodruin]

Why couldn't anyone just simply say that an arc length is needed to be found.

So I'm guessing, in my triangle drawing, the red line isn't what I needed to find, right?
That means the answer given here was incorrect, no?

No, it is not incorrect. Unlike your statement here, it clearly specifies "if one could burrow through the Earth".

I have made no definite statement on which is "correct" simply because I do not think your problem statement actually identifies which distance is intended. "Do not neglect the Earth curvature" could be taken to mean that you might compute the arc length if the straight segment was intended or vice versa.