- #1
Jbreezy
- 582
- 0
Homework Statement
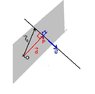
Say you have an equation of a line in 3 space and you want to find the distance from the line to the origin how do you go about it?
I guess by definition the distance of a line to a point ( say the origin in this case) is the minimum distance such that the line and some vector are perpendicular. That kind of sucks how I said it.
So x is a unique point on the line so you want the distance xo ( where o is the origin) such that xo is perpendicular to the line L . Not really sure how to do this. It is in the cross product section so maybe that would work. I tried to use dot product but I don't know how to get the shortest point. If I did I should dot xo with L and it would be 0. Well that was my thinking. I don't really know how to go about this.
Thanks