Distribution of force acting upon two charged objects

[NTL01]

Coulombs law states 2 point charges of opposite sign will attract where

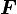acting simultaneously on two point charges

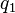and

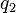as follows:

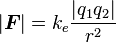
The formula calculates the force that will act and implies the force be equally experienced by both points of charge even if one charge is much greater than the other

In a vacuum , two such charges will move toward each other.

My first question is do they move at the same velocity and acceleration even though their charges are radically different in sign and strength.

Of course one stipulation of the law is that the charges are point charges and have no mass.

What if we complicate the problem by allowing each "entity" to have both charge and mass. Further let us say that q1 has large mass and low charge , and Q2 the opposite.

Question 2
Will the force F be experienced by both entities equally, or must the equation be re written to allow for some differential force with a lower value on q1 and a larger for q2 ( or possibly vice versa)

In a vacuum , what will motion look like.One would assume the smaller mass Q2 will be accelerated at a higher rate and move toward the larger mass at a much higher velocity and the large mass Q1 will hardly move at all

Is that what happens , or does the F get distributed in FAVOR of Q1 so the acceleration and velocity are normalized despite the difference in mass.?

 

[laner]

I don't know if there's a good way to talk about forces and accelerations together without talking about mass. You don't need to have massless point charges for Coulombs law to be applicable. It just says you have two point charges separated by a distance, here's the magnitude and direction of the force between those charges. You can easily just set the left hand side of that equation to $F=ma$ and just calculate the acceleration assuming whatever mass you want. But say that you had two point charges of equivalent mass that you don't care about. Their accelerations would be equal in magnitude and opposite in direction, ie: Newtons 3rd law, regardless of the magnitude of each individual charge. When you take changing mass into account you just simply calculate acceleration for each particle from Newtons 2nd law, which then describes the motion.

A good analogy is the force of gravity the Earth exerts on a falling body like a parachutist. The magnitude of the gravitational force acting on the parachutist, pulling them towards the Earth, is the exact same as the magnitude of the gravitational force acting on the Earth, pulling it towards the parachutist: $G\frac{M_{earth}m_{parachutist}}{r^2}$. But the mass of the Earth will be something like 22 orders of magnitude greater than the mass of the parachutist. So while the parachutist undergoes the familiar 9.8ms^-2 acceleration, the Earth only budges a tiny unmeasurable amount, again from $F=ma$.

I think you might be getting hung up on point charges. They're just a convenience people use when calculating these type of forces and they aren't real in this sense. If you give a point charge a mass it doesn't automatically become infinitely dense or something, you just say its a point in space that has mass and charge and go about doing physics with it.

 

[UncertaintyAjay]

This is the first I've heard of massless point charges. Point charges are assumed so that things such as the distribution of charge throughout he volume of the object do not need to be considered. Also, the force on the two charges will definitely be equal irrespective of their charges and this much is evident from Newton's 3rd Law.

 

[NTL01]

Thank you both Ajay and Laner

Laners gravitation analogy really did the trick for me.

It got me wondering about magnets, which in attract mode ( opposite polarities) follow a very similar inverse square and scalar as electrostatics

Would we figure/ do we know if the distribution of force is identical between two dissimilar strength magnets for the same reasons?

The shape of the field is different when two magnets oppose each other than two point charges becasue the field of each magnet folds back into itself to form a "circuit"

Does the filed shape alter the force distribution in any way?