Divergence Theorem Question (Gauss' Law?)

[vector013]

If F(x,y,z) is continuous and

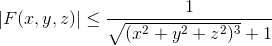for all (x,y,z), show that R3

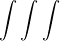
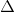dot F dV = 0

I have been working on this problem all day, and I'm honestly not sure how to proceed. The hint given on this problem is, "Take B_{r to be a ball of radius r centered at the origin, apply divergence theorem, and let the radius tend to infinity." I tried letting F = 1/((x² +y²+z²)^(3/2))+1), and taking the divergence of that, but it didn't really seem to get me anywhere. If anyone has any suggestions for at least how to set up this proof, I would really appreciate it.}

 

[ShayanJ]

Well, from the title it seems that you know you should use divergence theorem. So why don't you?

 

[HallsofIvy]

Since your region of integration is a ball and the integrand involves $x^2+ y^2+ z^2$, I would recommend changing to spherical coordinates to do that integration over the surface of the ball.

 

[vector013]

Spherical was my thought too. I guess what's been confusing me is that the vector field isn't explicitly given; there's just the inequality which indicates it exists at (0,0,0). My thought was to use Gauss' Theorem for Divergence in Spherical Coordinates: div F = 1/p²*d/dp*(p²F_p)+1/(psin(phi))*d/dphi*(sin(phi)F_phi + 1/(psin(phi))*dF_theta/dtheta. Since you have 1/p terms, div F would go to zero as the radius, p, goes to infinity. Therefore, the integral of 0 is 0.

 

[ShayanJ]

Spherical was my thought too. I guess what's been confusing me is that the vector field isn't explicitly given; there's just the inequality which indicates it exists at (0,0,0). My thought was to use Gauss' Theorem for Divergence in Spherical Coordinates: div F = 1/p²*d/dp*(p²F_p)+1/(psin(phi))*d/dphi*(sin(phi)F_phi + 1/(psin(phi))*dF_theta/dtheta. Since you have 1/p terms, div F would go to zero as the radius, p, goes to infinity. Therefore, the integral of 0 is 0.

I don't see any application of divergence theorem in your explanation. This is how it should be:
$\int_V \nabla\cdot \vec F dV=\int_{\partial V} \vec F \cdot \hat n dA$
Where $\partial V$ is the boundary of V. Now because in the surface integral, F is evaluated only at the boundary and the boundary is at infinity and we know that F is smaller than a function which goes to zero at infinity, the integral should be zero.

 

[vector013]

Oh okay, that makes sense. I didn't even think of it that way. Thank you so much for the suggestion!