Sollicitans said:
I noticed that you probably think I know what equations to use or how to apply the law. Truth is, I don't even know where you start from - not only is this case.
okay we all started from there
Sollicitans said:
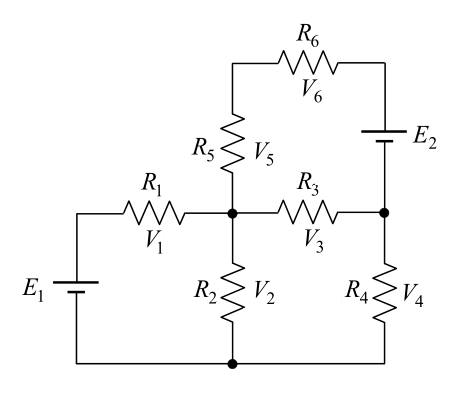
Can you or anyone point out the procedure I should follow if the circuit had no symbols at all? Here; I erased everything.
I think Hesch did that for you in post 10
here it is again, perhaps a little more cookbook
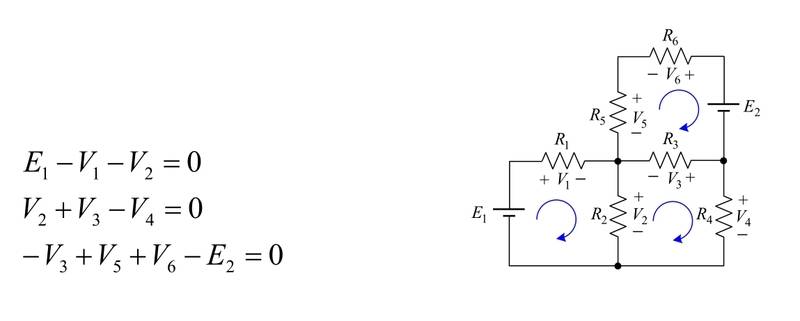
What: Arrive at the equations for KVL
How:
1. Assume directions of polarities and current flow.
2. Imagine yourself a tiny particle of current and walk the loops, writing down the first polarity sign you encounter for each voltage .
3. Solve the resulting algebraic equations.
Step 1:
i removed some more stuff from your drawing.
Note all +'s are left or up
all currents circulate CW
that's just assumed
any that were assumed wrong will have negative value at the end of (proper) calculations.
If you're sloppy you'll miss a sign. That's why it is necessary for a klutz like me to work them over and over until i get same answer 3 times in a row.
Okay, step 2:
inject yourself in the circuit at some convenient spot, maybe lower left corner and walk the circuit. I'll just follow I1.
Writing down the voltages i encounter, using first sign, i get
-E1 + I1R1 + (I1-I3)R2 = 0
Why did i write (I1-I3)R2 ? Because I1 and I3flow opposite directions so (their difference ) X R2 is the voltage. Were I3 also flowing down it'd be their sum.Next inject yourself in lower right corner and walk I3's path
-(I1-I3)R2 + (I3-I2)R3 +I3R4 = 0
and top right corner walking I2's path
+E2 -(I3-I2)R3 -I2R5 + I2R6 = 0
step 3:
If you know the resistor values and E1 & E2
then you have 3 equations and 3 unknowns
-E1 + I1R1 + (I1-I3)R2 = 0
-(I1-I3)R2 + (I3-I2)R3 +I3R4 = 0
+E2 -(I3-I2)R3 -I2R5 + I2R6 = 0
so it's 9th grade algebra from there.we used to say "plug and chug"..
i hope i did that right - been fifty years now ...
Would somebody younger check me above for flipped signs ?
thanks,
old jim