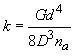bobfei
- 29
- 0
Hi,

Does a compression spring’s pitch or rise angle have any relation with its spring constant k?
I checked various sources and they differ on this. Some sites simply asks you to feed input into a simple formula:
On the other hand, some other sites require knowing the pitch between each winding, or equivalently rise angle θ, and result varies with different pitch/θ even all four parameters above remain unchanged. An example is at http://www.planetspring.com/pages/compression-spring-calculator-coil-calculator.php?id=compression.
I strongly suspect the first type of treatment above is incorrect. Consider extreme case:
It is then quite clear that θ cannot be overlooked, and the first kind of treatment above is obviously wrong.
I wonder why so many websites are still providing that answer? Could someone help or give a derivation of the compression spring k formula?
Bob
Does a compression spring’s pitch or rise angle have any relation with its spring constant k?
I checked various sources and they differ on this. Some sites simply asks you to feed input into a simple formula:
k=Gd4/3D3na
in which k: spring constant
G: material’s shear modulus
d: diameter of the wire
D: outer diameter of each winding
An example of this treatment can be found at http://www.efunda.com/DesignStandards/springs/calc_comp_designer_eqn.cfm.G: material’s shear modulus
d: diameter of the wire
D: outer diameter of each winding
On the other hand, some other sites require knowing the pitch between each winding, or equivalently rise angle θ, and result varies with different pitch/θ even all four parameters above remain unchanged. An example is at http://www.planetspring.com/pages/compression-spring-calculator-coil-calculator.php?id=compression.
I strongly suspect the first type of treatment above is incorrect. Consider extreme case:
1. θ →0° : This means we are not winding the spring up so all windings remains on the same plane. Of course when approaching this extreme k would approach zero.
2.. θ →90°: This corresponding the case when we are pulling the string straight without any winding and it points straight upward. Trying to compressing such a “spring” on the two ends is like compressing a stick rod, and we would get extremely large resistance due
to the rigidity of the material itself. Obviously in this case k → infinity
2.. θ →90°: This corresponding the case when we are pulling the string straight without any winding and it points straight upward. Trying to compressing such a “spring” on the two ends is like compressing a stick rod, and we would get extremely large resistance due
to the rigidity of the material itself. Obviously in this case k → infinity
It is then quite clear that θ cannot be overlooked, and the first kind of treatment above is obviously wrong.
I wonder why so many websites are still providing that answer? Could someone help or give a derivation of the compression spring k formula?
Bob