StephenSLR
- 2
- 0
Hi all,
I'm having an online discussion and curious to know about the forces a 3-point seat belt has on a car.
One guy is fitting this retractable belt to his car.

The retractor and anchor mount at one bolt hole, the anchor is off centre, it attaches via a steel extension piece, the section of extension piece you can't see is behind the retractor and bolted to the same hole the retractor is.
His car has two 'factory installed' lower mounting holes on one side, a separate hole each for the retractor and anchor and I advised him to mount the belt as it is here.
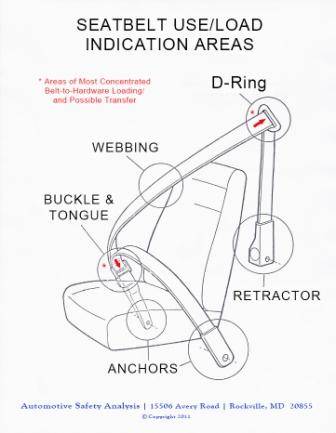
Saying 'Personally I'd use the factory bolt hole, in an accident you have the force distributed between four anchor points not three'
I received a reply from someone saying
the force isn't divided up between four anchor points, it's really only three, the two floor ones on the side of the car and the one on the trans tunnel side.
The tunnel side gets 50% and the side ones 25% each
The top mount at the D-ring definitely experiences force so let's say you remove it.
Wouldn't the bottom anchor bolts feel an increase in force? When the person in the car experiences a sudden stop, doesn't the resultant force that the car experiences from the seat belt remain the same in both lap belt and lap-sash belt applications?
My opponent says adding an extra bolt will not distribute the forces evenly but I think he is assuming the tension T will be the same in both seat belt applications.
s
I'm having an online discussion and curious to know about the forces a 3-point seat belt has on a car.
One guy is fitting this retractable belt to his car.
The retractor and anchor mount at one bolt hole, the anchor is off centre, it attaches via a steel extension piece, the section of extension piece you can't see is behind the retractor and bolted to the same hole the retractor is.
His car has two 'factory installed' lower mounting holes on one side, a separate hole each for the retractor and anchor and I advised him to mount the belt as it is here.
Saying 'Personally I'd use the factory bolt hole, in an accident you have the force distributed between four anchor points not three'
I received a reply from someone saying
the force isn't divided up between four anchor points, it's really only three, the two floor ones on the side of the car and the one on the trans tunnel side.
The tunnel side gets 50% and the side ones 25% each
The top mount at the D-ring definitely experiences force so let's say you remove it.
Wouldn't the bottom anchor bolts feel an increase in force? When the person in the car experiences a sudden stop, doesn't the resultant force that the car experiences from the seat belt remain the same in both lap belt and lap-sash belt applications?
My opponent says adding an extra bolt will not distribute the forces evenly but I think he is assuming the tension T will be the same in both seat belt applications.
s
Last edited: