Does an electron with negative electrostatic potential energy fall up?

[Wnt]

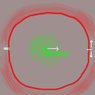
In a vacuum under standard gravity, an anchored spherical metal electrode is brought to +1,000,000 volts relative to the distant walls of a much larger chamber. (I'm a new user; hopefully this will display as attachment 1) Therefore, electrons that fall through a small gap in the electrode potentially emit kinetic energy greater than their 0.5 MeV rest mass. This energy comes from the electrostatic field that surrounds the spherical electrode (red haze; the energy in this field is proportional to the square of the magnitude of the force outward from the electrode, which is reduced by the negative charge of the electron inside). Within the sphere, there is no electrostatic field except that from the electron itself (green haze).

In this scenario, an electron is emitted from just outside the positive electrode so that it falls slowly through the center of the sphere, where it should experience no force from the shell of positive charge that surrounds it. The question is, as it crosses the chamber, will it strike ABOVE or BELOW the mark?

a) Gravity will pull the electrode downward according to its normal rest mass, like any particle; it is a curvature of space. As a consequence, it will force the center of mass of the electrostatic field in red to move upward.
b) Gravity will pull the electrostatic field downward, forcing the electron to move upward and strike above the mark.

And of course there's always c) you can tell me it's far, far more complicated than that. :)

 

[Khashishi]

a.
Since there is no field in the electrode (other than the electron itself), the only force acting on the electron is gravity. The complicated setup is irrelevant here.

Potential is just some kind of bookkeeping system and isn't as real as the fields.

 

[Khashishi]

So, you probably are wondering about the mass of the entire system. If the total mass of the exterior walls and electrode is M, and the mass of the electron is m_e, then what if you drop the electron from the exterior wall to the electrode. Assume the exterior walls are anchored to the electrode. Then the electron gains a large momentum toward the right, and the walls+electrode gain an equal momentum to the left. The total system has zero momentum, and the total energy must be conserved. Since the total momentum is zero, the total energy is $E=(M+m_e)c^2$.

Ok, now for some fun. As the electron accelerates toward the center, it emits some EM radiation. The rest of the system also accelerates a little and emits some radiation. Now what happens? Clearly, if the EM radiation leaves the system, the total energy of the system must now be less than (M+m_e)c^2. This is possible because the density of the electromagnetic field is decreased slightly. $E_{EM}=\frac{1}{2}\epsilon E^2 + \frac{1}{2\mu} B^2$.

Ok, so where is this electromagnetic field mass actually located? Since the energy is lower than before, the new mass must be lower than (M+m_e). But how? For the same reason a bound atom weighs a little less than the nucleus + electrons. I don't think it's possible to divide the mass of the bound system among the constituent particles, since the constituent particles no longer exist as solo objects once they are bound.

I still say a is correct for above despite this complication.