greypilgrim
- 579
- 44
Hi.
This picture shows an iron ring shielding a static magnetic field:
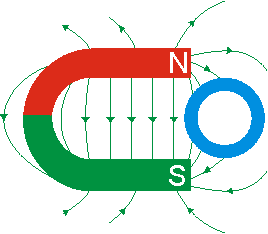
Does this really work, and why? I know that a conductor can shield an electric field (Faraday cage) and a changing magnetic field (Lenz's law), but why would it shield a static field? Especially since iron is a ferromagnet.
This picture shows an iron ring shielding a static magnetic field:
Does this really work, and why? I know that a conductor can shield an electric field (Faraday cage) and a changing magnetic field (Lenz's law), but why would it shield a static field? Especially since iron is a ferromagnet.
