Does the addition of a new vertex always guarantee a Hamiltonian path or cycle?

[atrus_ovis]

Watching this lecture from nptel about NP completeness:
http://www.youtube.com/watch?v=76n4BjlL1cs&feature=player_embedded

-We have an algorithm, HC , which given a graph tells us whether or not it has a hamiltonian cycle.
-We want to use it in order to create an algorithm that determines whether an input graph has a hamiltonian path.


If the input has a HC, then it has a HP as well.Okay.

But around 29:00, it is stated:

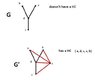
If the input doesn't have a HC (the output of HC algorithm is a "no"), we add a vertex to it that connects to all other vertices in the graph.If that new gragh G' has a HC, then the original graph G has a HP.
But thinking about this, how bout this example?

edit:in the pic, i meant to say that "graph G doesn't have a HP"

 

[Edgardo]

You've misunderstood what the goal is. The goal is to find out whether G has a HP.
See: http://www.youtube.com/watch?v=76n4BjlL1cs&feature=youtu.be#t=21m08s"

The input is the Graph G' which consists of the original Graph G and the additional vertex u connected to all vertices of G.

We want to find out if G has a HP by using the following theorem:
G has a HP iff G' has a HC

In your example, let us pretend that we do not know whether G has a HP.
So, we form G' and use it as an input for HC. Now, there are two possible outcomes:
(i) HC says: yes, G' has a HC. It then follows that G has an HP.
(ii) HC says: no, G' has no HC. It then follows that G has no HP.