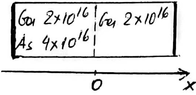Donor and Acceptor Concentrations in a Si speciment

[lelouch_v1]

Homework Statement:

Suppose that we have a Si speciment and there are Ga atom impurities of $2*10^{16} \text{cm}^{-3} $.`Then, at the left side we insert As impurity atoms of $4*10^{16} \text{cm}^{-3}$. A pn junction is created. What are $N_D$ and $N_A$ at each side of the junction?

Relevant Equations:

$$n = \vert{N_D - N_A}\vert$$

At the left side we have the n-side of the junction, whereas at the right we have the p-side. I am a little confused over $N_D$ and $N_A$ at the n-side. Do the Ga atoms interact with the As ones, so we have $N_D = 2*10^{16} \text{cm}^{-3}$, or not, ans thus we have $N_A=2*10^{16} \text{cm}^{-3}$ and $N_D = 4*10^{16} \text{cm}^{-3}$ ?