Don't understand Stoke's Theorem (Revised)

[iScience]

Moderators: For some reason I couldn't edit/delete my last post on Stoke's Thrm. I've revised the question for clarity; please delete the other post. Thanks!


I'm trying to get an intuition on Stoke's Theorem, and all explanations I found use this same argument:
-------
On a given surface (image below), the curl field at each surface element cancels with the curl field of its neighbors, and the only curl fields that don't get canceled are at the surface boundary.
-------

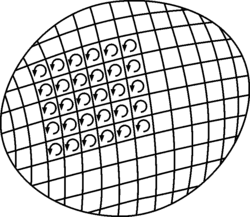
Main problem i have with this is, i don't understand what those curls are representing.
Say i have a vector field in R-2 with a non-zero curl. well, if i were to graph its curl field, i would be seeing a bunch of parallel vectors (the curl vector), not a bunch of circulating vectors. This makes me think that those circulating vectors aren't those of the curl field's, but rather those of the original vector field's.
On the other hand, Stoke's theorem mentions the sum of the curl field vectors, not those of the original vector field. See my conundrum?
So are the circulating vectors in the image referring to the original vector field's or the curl field's?


Thanks in advance

 

[homeomorphic]

In that picture, what you would do to get those circulation thingies is to dot the normal vector of the surface with the curl vector. The curl vectors don't really give you circulation until you dot them with a normal vector.

The little circulation arrows are measuring how much the original vector field circulates.

It's kind of like an angular momentum vector. The vector just gives you the axis of rotation and its magnitude is proportional to the angular momentum. It's just like that.

 

[iScience]

I still don't understand where the circulating vectors come from. If that is supposed to be a vector field it looks like it's discontinuous everywhere. Shouldn't a vector field look something more like this?

The little circulation arrows are measuring how much the original vector field circulates.

Consider the surface in this R-2 vector field. At various regions within the surface, the curvature (which is what the curl measures) varies. For instance, region A vs region B

the magnitude of the curl field (in \hat{z}) is not uniform throughout the surface because of the changing curvature. So even if this vector field could somehow be represented as individual circulations, the curl value at any given point within the surface would not be the same as the curl values of its neighbors'. how then is the cancellation done?

 

[Stephen Tashi]

Drawing contours to represent the vectors in a vector field is ambiguous because a contour can't convey the both the direction and magnitude of the field at a given point. That's why when vector fields are represented by contours, the contours usually show curves of equipotential and the equipotential curves don't run in the direction of the field vectors. Your questioning of the "circulation vector" portrayal of Stokes theorem is justified. I think most people use it as visual reminder of Stokes theorem ( in the same manner that people use verbal jingles to remember mathematical facts) rather than as a guide for how to prove it.

Stokes theorem states the equality of two scalars, not the equality of two vectors. So, as homeomorphic pointed out, if we want to use the circulation vectors picture to explain Stokes theorem, we need to relate the picture to a sum of scalars.