Doubts on angular momentum [master's degree exam]

[Raphael M]

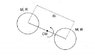
Two hollow spheres, both the mass and radius R M , which are rotating around a center of mass ( CM ) , with an initial period T_o, are kept distant from each other by an ideal wire with a distance of 8R. At a given instant a motor is driven by wrapping the wire and making the two spheres meet. Consider the inertia moment motor despicable , and disregard the effects of gravity . Express all your results in terms of M, R and T_o. Consider the angular momentum of the spherical shell 2 / 3MR²

a) determine the angular momentum of the system relative to the center of mass of time before the engine is started .

b ) determining the angular velocity of rotation at the time when a ball contacts the other
I Solved the a) like this

L = I.w
L = (2/3 MR²) . (2π(4R))/T₀.(4R)
L = (4/3 MR²)/ T₀

that's the angular momentum for 1 shell. multiply that by 2 to get the angular momentum to the sistem.

L = (8/3 MR²)/T₀

But I can't solve the B part. I've tried everything I could, but I can't make the angular velocity at the contact situation in terms of T₀.Help please ;)...
sorry about my english. I'm not fluent.

 

[Doc Al]

I Solved the a) like this

L = I.w
L = (2/3 MR²) . (2π(4R))/T0.(4R)
L = (4/3 MR²)/ T0

You need the moment of inertia of each sphere about the axis of rotation. Use the parallel axis theorem.