EebamXela
- 16
- 0
I've been fooling around in MS Excel trying to reconstruct this fractal:

I haven't had any issues here making it. I totally understand the algorithm for generating the left turn/right turn ordering. What I really want to know is how this version is generated:
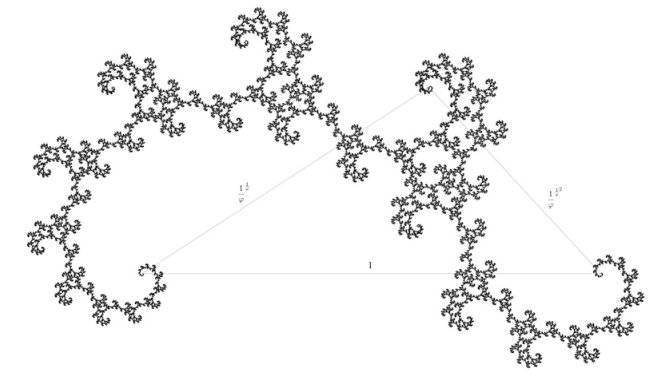
Original image: http://en.wikipedia.org/wiki/File:Phi_glito.png
The sides of the base triangle are equal to:
1.000000000
0.742742945
0.551667082
Is this fractal generated using the same algorithm as the above one? I can't seem to find any explanations anywhere to confirm. I tried using the same algorithm and steps to recreate it in excel but all i get is a fractal that KINDA looks like it, but it's obviously not:
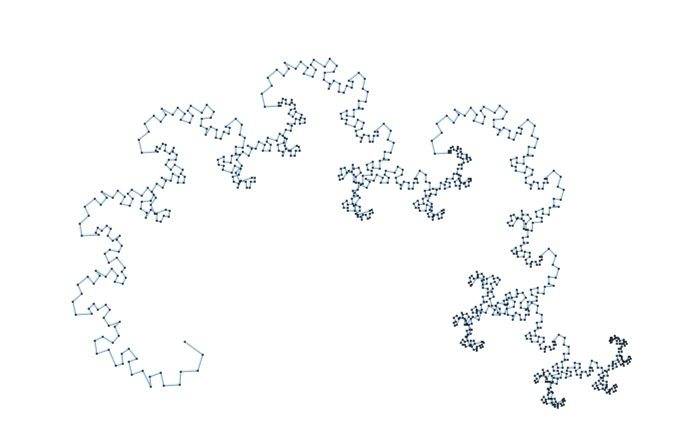
I don't have any code to share because I'm not very good with code. I figured once i nail down how to actually construct the thing manually i'd try coding it.
Please someone tell me what I'm doing wrong. Thanks.
I haven't had any issues here making it. I totally understand the algorithm for generating the left turn/right turn ordering. What I really want to know is how this version is generated:
Original image: http://en.wikipedia.org/wiki/File:Phi_glito.png
The sides of the base triangle are equal to:
1.000000000
0.742742945
0.551667082
Is this fractal generated using the same algorithm as the above one? I can't seem to find any explanations anywhere to confirm. I tried using the same algorithm and steps to recreate it in excel but all i get is a fractal that KINDA looks like it, but it's obviously not:
I don't have any code to share because I'm not very good with code. I figured once i nail down how to actually construct the thing manually i'd try coding it.
Please someone tell me what I'm doing wrong. Thanks.