mathmari
Gold Member
MHB
- 4,984
- 7
Hey! :giggle:
Make a drawing for each of the values of the angle below indicating the angle at the unit circle (in other words: $\text{exp} (i \phi )$) and its sine, show cosine, tangent and cotangent.
Give these four values explicitly in every case (you are allowed to use elementary geometry and the Pythagorean theorem).
$$\phi=\frac{\pi}{6}, \ \ \phi=\frac{\pi}{4}, \ \ \phi=\frac{2\pi}{3}, \ \ \phi=\frac{5\pi}{6}, \ \ \phi=-\frac{2\pi}{3}, \ \ \phi=-\frac{\pi}{3}$$
So at a unit circle we draw an angle $\phi$ and then we get a drawing like the following, right? But what does it mean to give these four values explicitly? :unsure:
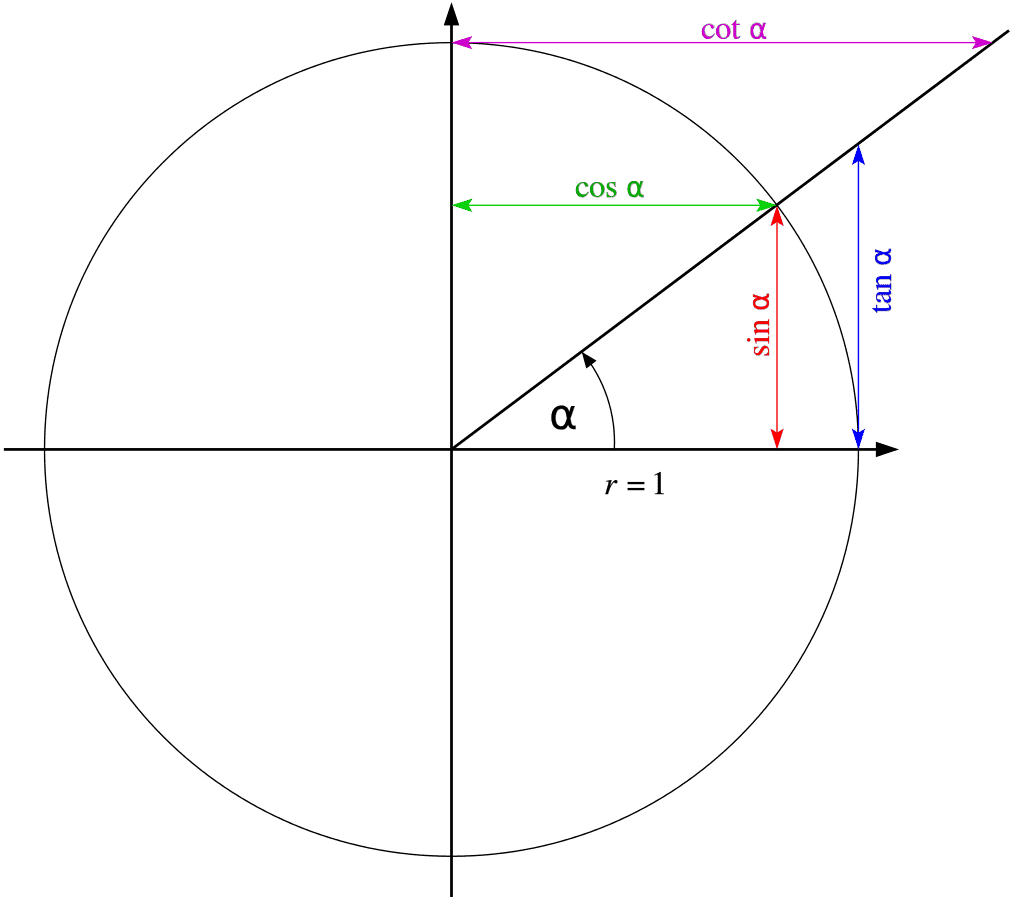
Make a drawing for each of the values of the angle below indicating the angle at the unit circle (in other words: $\text{exp} (i \phi )$) and its sine, show cosine, tangent and cotangent.
Give these four values explicitly in every case (you are allowed to use elementary geometry and the Pythagorean theorem).
$$\phi=\frac{\pi}{6}, \ \ \phi=\frac{\pi}{4}, \ \ \phi=\frac{2\pi}{3}, \ \ \phi=\frac{5\pi}{6}, \ \ \phi=-\frac{2\pi}{3}, \ \ \phi=-\frac{\pi}{3}$$
So at a unit circle we draw an angle $\phi$ and then we get a drawing like the following, right? But what does it mean to give these four values explicitly? :unsure: