rndaryam
- 3
- 0
https://postimg.org/image/z96a0jn8b/ https://postimg.org/image/z96a0jn8b/
link to image (bcs the feature doesn't work): https://postimg.org/image/z96a0jn8b/
1. Homework Statement
A cannon (mass m_c) is standing on the ground before it fires a cannon ball (mass m_b). At the time t_0=0. the cannon ball is leaviing the gun at height h_m above the ground with velocity V_0 at angle alpha. Air resistance can be neglected.
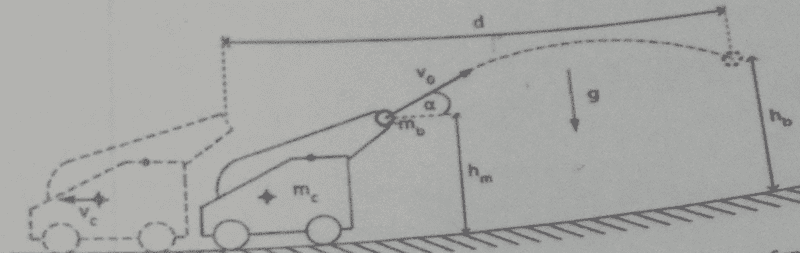
Find:
1. V_c(m_b,m_c,V_o,alpha)
2. h_b(t)
3. d(t)
This is my attempt for question 1:
we use F=m.a for only the horizontal direction and I got Vc=m_b.v_0.cos alpha / mc. Anyone can help me to solve the 2nd and 3rd question? I would appreciate it a lot. Thanks
link to image (bcs the feature doesn't work): https://postimg.org/image/z96a0jn8b/
1. Homework Statement
A cannon (mass m_c) is standing on the ground before it fires a cannon ball (mass m_b). At the time t_0=0. the cannon ball is leaviing the gun at height h_m above the ground with velocity V_0 at angle alpha. Air resistance can be neglected.
Homework Equations
Find:
1. V_c(m_b,m_c,V_o,alpha)
2. h_b(t)
3. d(t)
The Attempt at a Solution
This is my attempt for question 1:
we use F=m.a for only the horizontal direction and I got Vc=m_b.v_0.cos alpha / mc. Anyone can help me to solve the 2nd and 3rd question? I would appreciate it a lot. Thanks
Last edited: