ok, I've
had some help 
, and i think the answer is this …
the
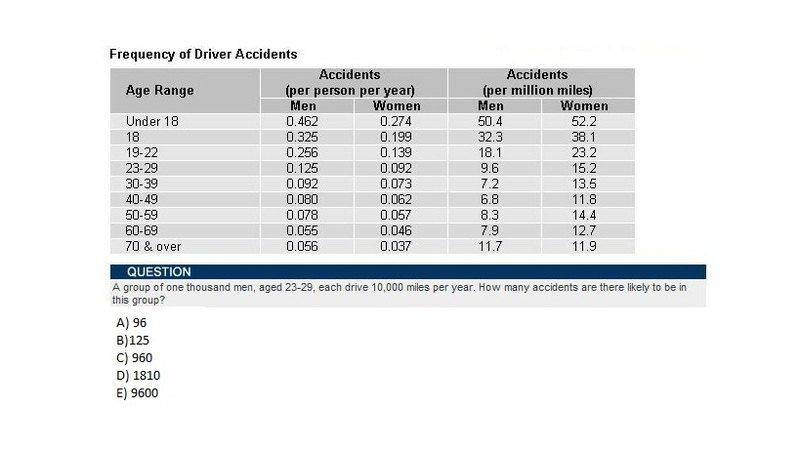
primary statistic is the number of accidents per mile, simply because, for any particular driver, we expect accidents to depend on mileage rather than on time …
assuming accidents are random, if you drive twice as far, you should have (roughly) twice as many accidents
(of course, there will be exceptions … for example, if someone is a very good driver, but has accidents when he gets drunk, then his accident rate will be proportional to the number of times he gets drunk, which presumably depends on time rather than on mileage … also, a lot of accidents happen very close to the beginning and end of a journey, so someone prone to those will have an accident rate proportional to the number of journeys, not to the length of the journeys …
but i think the question expects you to assume that most accidents do depend on mileage)
in that case, the rate per mile is the
primary statistic, and any observed rate per year will be a less reliable secondary statistic to be used only if you can't use the primary one
hmm … that doesn't
entirely convince me

… but I'm pretty sure it's what the examiners intended

 ...
...