congo
- 3
- 0
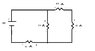
Can someone help me solve this problem using matrices and not Kirchhoff's rules. My professor posted this as a challenge question and I would like to know how to solve such a problem. Please help! I tried looking up how to solve this type of problem using matrices but to no luck. I don't know where to even begin with this question. Here's what the circuit looks like. Any help is greatly appreciated. Thank You!
I did this question using kirchhoff's rule and I would like to know how to solve this using matrices. Please guide me on how use matrices to get to the answers.
I did this question using kirchhoff's rule and I would like to know how to solve this using matrices. Please guide me on how use matrices to get to the answers.