Discussion Overview
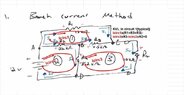
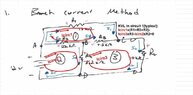
The discussion revolves around solving a circuit analysis problem involving simultaneous equations derived from Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL). Participants are attempting to determine unknown branch currents in an electrical circuit.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses confusion about how to proceed after obtaining 7 equations and 6 unknowns, specifically questioning how to reduce the equations to a solvable form.
- Another participant suggests that having 3 KCL equations should suffice to determine the currents, implying that fewer equations might be needed.
- A third participant explains the relationship between KCL and KVL equations, indicating that it is acceptable to have more equations than unknowns and suggesting a method to eliminate variables to simplify the problem.
- One participant advises trying a simpler version of the problem to gain clarity and emphasizes the importance of showing work for better assistance.
- Another participant points out that the KCL equations are not independent and suggests a method to reduce the system to three equations and three unknowns by selecting specific currents.
- There is a brief interjection indicating a potential error in KVL application, but no further details are provided.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to simplify the equations or the independence of the KCL equations. Multiple competing views on how to proceed with the problem remain evident.
Contextual Notes
Participants mention the need to express some currents in terms of others, indicating potential dependencies and assumptions that may not be fully articulated. The discussion reflects varying levels of understanding regarding the relationships between equations.
Who May Find This Useful
This discussion may be useful for students or practitioners in electrical engineering or circuit analysis who are grappling with similar problems involving simultaneous equations and the application of KCL and KVL.