- #1
PhiowPhi
- 203
- 8
Given the following diagram:
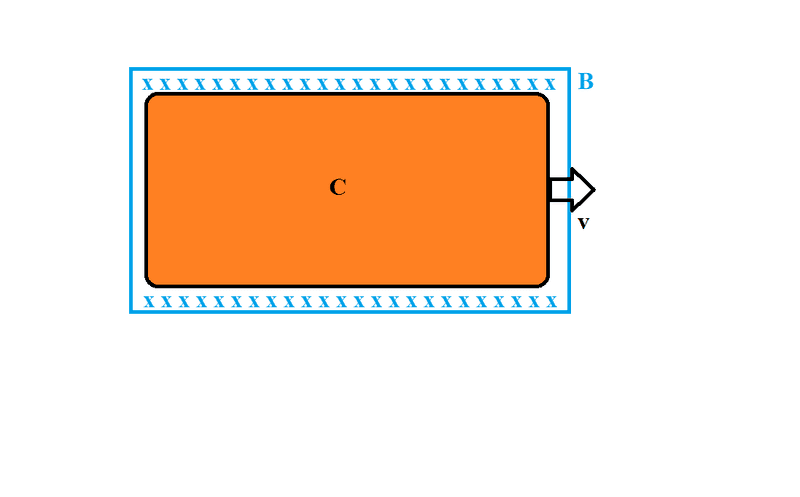
The conductor(C) of known volume(##V##) and resistance(##R##), passes a uniform magnetic field(##B##)at a constant velocity(##v##), via the following formula: ## \epsilon = -vBL## the induced EMF can be calculated. This conductor acts as a power source to a certain circuit,therefore, it's connected to a circuit(which I chose not to include in the diagrams because I am focusing on this conductor specifically) to distinguish the resistances I'd like to label ##R## as the internal resistance of the power source( that is the conductor) and r as the resistance of the circuit.
I think the way of calculating the induced current here is simply Ohm's law:
##I = \frac{V}{R + r}##
the total resistance is it ##(r+R)##, not sure though...
Now, the main point, what would be the effect of reducing the magnetic field span(Magnetic field span: the area the magnetic field covers at the same strength) like so:
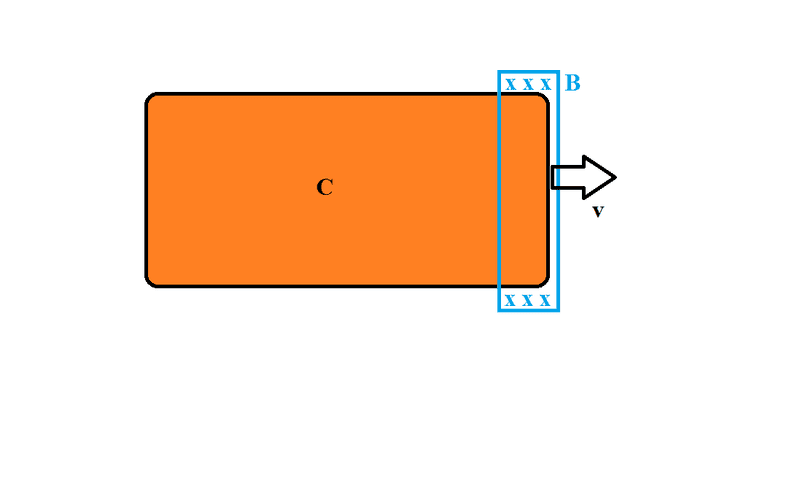
While ##L##, ##v## , and ##B## are all the same? My assumption: that the induced EMF is the same, however, the second diagram/version would induced a lower current? But why...?
It makes no sense to me that the the currents would be the same magnitude, it does in-terms of EMF because of all the variables in the motional EMF formula are the same.
The conductor(C) of known volume(##V##) and resistance(##R##), passes a uniform magnetic field(##B##)at a constant velocity(##v##), via the following formula: ## \epsilon = -vBL## the induced EMF can be calculated. This conductor acts as a power source to a certain circuit,therefore, it's connected to a circuit(which I chose not to include in the diagrams because I am focusing on this conductor specifically) to distinguish the resistances I'd like to label ##R## as the internal resistance of the power source( that is the conductor) and r as the resistance of the circuit.
I think the way of calculating the induced current here is simply Ohm's law:
##I = \frac{V}{R + r}##
the total resistance is it ##(r+R)##, not sure though...
Now, the main point, what would be the effect of reducing the magnetic field span(Magnetic field span: the area the magnetic field covers at the same strength) like so:
While ##L##, ##v## , and ##B## are all the same? My assumption: that the induced EMF is the same, however, the second diagram/version would induced a lower current? But why...?
It makes no sense to me that the the currents would be the same magnitude, it does in-terms of EMF because of all the variables in the motional EMF formula are the same.
 ).
).