John004
- 37
- 0
Homework Statement
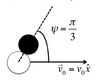
A super cue ball is made of the same material with the target ball (radius r) but slightly larger: rc = (3)^(1/3)*r The cue ball collides with the target ball on a frictionless table, as shown below, with initial speed of v0. The collision is not head-on, as shown below.
a) What are the velocities of the two balls after the collision? You need to determine both the speeds and directions!
b) In the CM frame, what is the target ball’s direction, relative to the x-axis?
Homework Equations
ρ = m/V
ρ = 4/3 π r3
The Attempt at a Solution
[/B]
so for the masses,
m1 = ρV1 , m2 = ρV2
taking the ratio of those guys gives m1 = 3 m2
if i use conservation of linear momentum and kinetic energy conservation, i end up with two sets of equations but one is a vector equation and the other is not, so i don't know how to even start this problem
Attachments
Last edited: