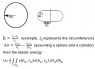
This is a very complicated problem that has very little practical applicability. Are you sure that you want to work on this, given that there are many other simpler problems that have practical applicability?
I would start by developing the strain energy equation for the rubber as a function of the three principal stretches. The rubber deformations in your application may be large, so you can't use the small strain approximations to describe the rubber elasticity behavior, and you can't use a one dimensional version because the local deformations are going to be 3D.
The behavior the the glass bead gravel inside the ball is going to be complicated, so you can start out by researching the rheological behavior of non-consolidated granular solids.
Temporarily, before including the glass bead behavior in the model, you should consider assuming there is air inside. At least then the behavior of the material inside the ball would be simple to include. You can switch to granular beads later.
You also need to start formulating the stress equilibrium equations for the rubber cover, treating either as a membrane or a shell. A membrane is, of course easier to solve.