- #1
Titan97
Gold Member
- 450
- 18
If there is a small object with positive charge placed above a metal plate, the object induces a negative charge on the surface of the plate facing the object. Let's call this surface as S1.
(The metal plate is initially uncharged).
But from conservation of charge, the net charge in a metal plate has to be zero. So the surface below S1 will get a positive charge.
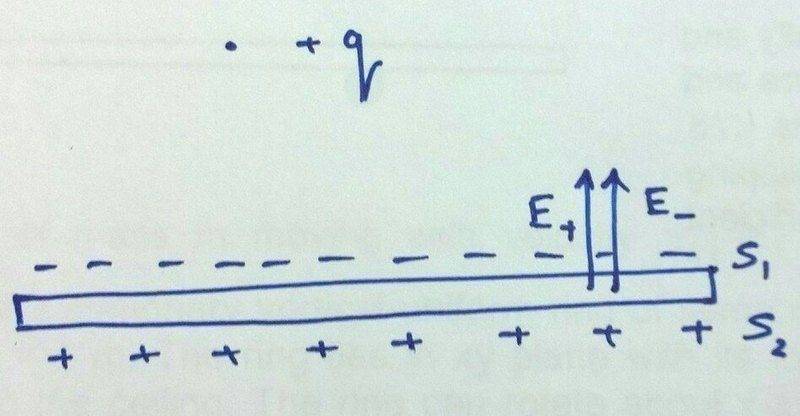
But from the above picture, the field due to S1 and S2 are along the same direction and they don't cancel out. So how is electric field inside a conductor zero? Is it because of the electric field due to the object?
(The metal plate is initially uncharged).
But from conservation of charge, the net charge in a metal plate has to be zero. So the surface below S1 will get a positive charge.
But from the above picture, the field due to S1 and S2 are along the same direction and they don't cancel out. So how is electric field inside a conductor zero? Is it because of the electric field due to the object?
Last edited: