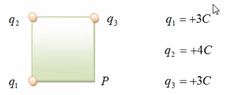- #1
emmanual
- 2
- 0
- Homework Statement
- Three point charges q1(+3C), q2(+4C), q3(+3C) are located in a square-shaped form with a distance of 2cm with a 90° cone in every edge(picture in the attached file 39png). Calculate the resultant intensity of point P.
- Relevant Equations
- Coulomb's law :
F=q1q2/4πεr2
Parallelogram law:
R=√(P²+ Q²+ 2PQcosα)
I've calculated the intensity for every point charge which are
EA = 6.741 x 10¹³ NC¯¹
EB = 4.494 x 10¹¹ NC¯¹
EC = 6.741 x 10¹³ NC¯¹
and I am pretty sure about this far but I am struggling to calculate the X-axis intensity and Y-axis intensity to find the entire approximate intensity with the parallelogram law.
PLEASE HELPPP!
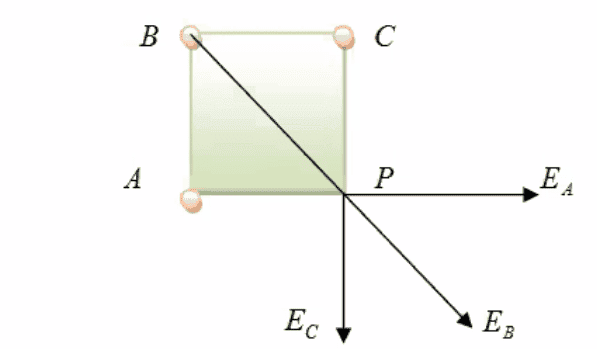
EA = 6.741 x 10¹³ NC¯¹
EB = 4.494 x 10¹¹ NC¯¹
EC = 6.741 x 10¹³ NC¯¹
and I am pretty sure about this far but I am struggling to calculate the X-axis intensity and Y-axis intensity to find the entire approximate intensity with the parallelogram law.
PLEASE HELPPP!