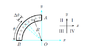
SUMMARY
The discussion focuses on calculating the x-component of the electric field at the origin due to a circular arc with a charge of 3.8 μC and a radius of 1.9 m. The relevant equations include E = kq/r², dq = λ dθ, and λ = Q/(R θ). The user attempted to integrate the expression kq/r² ∫sinθ/θ dθ but received an incorrect answer of 12968.1 N/C. The correct approach involves substituting the values for dq and ds into the expression for dE and integrating from θ = 0 to π/2.
PREREQUISITES
- Understanding of electric fields and Coulomb's law
- Familiarity with calculus, specifically integration techniques
- Knowledge of linear charge density (λ) and its calculation
- Basic principles of electrostatics and charge distribution
NEXT STEPS
- Review the derivation of electric fields from continuous charge distributions
- Practice integration techniques involving trigonometric functions
- Learn about the application of the Coulomb constant in electric field calculations
- Explore the concept of linear charge density and its implications in electrostatics
USEFUL FOR
Students studying electromagnetism, physics educators, and anyone involved in solving electrostatic problems related to charge distributions.