Electric field above the centre of a rectangle

[says]

Homework Statement

Exercise in integration: Using the Electric Field E of a straight line
segment of charge, find the electric field at height 10 cm above the centre of a
rectangle of sides 10cm and 20 cm carrying charge density 4 μC/m².

Homework Equations

µ=Q/L
µ = charge density
Q = total charge
L = length of line charge
μ = charge density = 4 μC/m²
E = 1/4πε₀ Q/r² - Electric Field surrounding point charge.

The Attempt at a Solution

Electric Field surrounding a point charge:
E = 1/4πε₀ Q/r²

Electric field at the location of a test charge q due to a small chunk of charge in the line dQ
dE = 1/4πε₀ dQ/r²

The amount of charge dQ can be restated in terms of charge density
dQ = μ dx

dE = 1/4πε₀ μ dx/r²

Change dx to dθ and sweep different angles and substitute dθ/a for dx/r²

dE = 1/4πε₀ μ dθ/a²

dEy = dE cosθ

dEy = 1/4πε₀ μ / a cosθ dθ

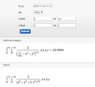
Ey = ∫ 1/4πε₀ μ / a cosθ dθ (with θ going from +θ to -θ)

Can I just do the same thing in the other direction and add the two? i.e.

Ex = ∫ 1/4πε₀ μ / a cosθ dθ (with θ going from +θ to -θ)

so

Ey + Ex = electric field at height above the rectangle?

The question said to use the 'Electric Field E of a straight line segment of charge' so I thought it just meant to break it up into two line segments. All I would need to do then is calculate the angles from each side of the rectangle.

 

[rude man]

The question said to use the 'Electric Field E of a straight line segment of charge' so I thought it just meant to break it up into two line segments. All I would need to do then is calculate the angles from each side of the rectangle.

I think you have the right idea but I'm not sure.
You're supposed to start with the dE field of a straight line of either 10 or 20 cm in length and differential width.
Then integrate (as the problem suggests) this line over the other dimension (if 10 cm line, +/- 10 cm; if 20 cm line, +/- 5 cm.)

 

[haruspex]

I thought it just meant to break it up into two line segments.

I read it as breaking the rectangle into thin parallel strips, treating each strip as a straight line of charge. I.e. just a standard dxdy integration, except that it assumes you already have the result for the first stage of integration.

With no description of what your x, y and θ represent, I cannot follow your working.

 

[says]

I tried a different approach.

r = √(x²/4 + y²/4+z²
dQ = λds
ds = (x + y)/ 2

V_E = λ / 4πε₀ ⋅ ds / √r

E = -∇V_E

E = -λ / 4πε₀ ( ∂ ds/dx x̄ + ∂ ds/dy ŷ + ∂ ds/dz ẑ )

E = -λ / 4πε₀ ( [-xy-y²+4z² / (x²+y²+4z²) ] x̄ - [x²-xy+4z² / (x²+y²+4z²) ] ŷ - 4-(x-y) / (x²+y²+4z²)^3/2 ẑ

substitute into the equation:
λ: 4*10^-6 c/m²
x = 0.10 m
y = 0.20 m
z = 0.10 m

E = -7.989 x̄ - 3.994 ŷ - 15.973 ẑ V/m

Not sure if I'm making this problem more complicated than it is though

 

[rude man]

h

You're not following instructions which are to use the expression for the E field from a line segment as basis for the solution. Why not do it that way?

But approaching it from a potential viewpoint would certainly be possible otherwise. I did not check your math though.

 

[says]

So if I use the line segment equation and then just sum up what I get for the x & y line.

The electric field, E, at the point, P, will be equal to the electric field at the line segment of x + the electric field at the line segment of y?

dE_z = (kλdx / r²) (z/r)
E_z= kλz ∫ dx / (z² + x²)^3/2
E_z= kλ / z [x / (z² + x²)^1/2]
E_z= kλ / z [b / (z² + b²)^1/2 + a / (z² + a²)^1/2]

for the x line: a=-0.05, b=0.05
for the y line: a=-0.10, b=+0.10
z=0.10
λ =4 μC/m²
k = 8.98 * 10⁹ N m² C^-2

 

[vela]

Do you know the expression for the electric field for a line of charge of length L a height z above the center?

 

[haruspex]

sum up what I get for the x & y line.

I do not know what you mean by the x and y lines. The charge density is given in terms of per unit area, so the charged object is a rectangular sheet, not just the outline of a rectangle. (Or have you stated the problem incorrectly?)
X and Y are the coordinates of points in the square.
Consider a strip of width dx from (x, -b, 0) to (x, b, 0). What is the charge on that strip? Using the formula for the field due to a uniform line of charge, what field does that exert at (0, 0, z)? What is the component of that field in the z direction?
To get the field due to the whole rectangle, you need to integrate wrt x.

 

[says]

Yes, I should've worded that better.

E=1/4πε₀ Q/r²

I got my equation from http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html

So the electric field at point P would have an x and y component and be equal to ______ N/C x̄, ______ N/C ŷ

 

[haruspex]

Yes, I should've worded that better.

E=1/4πε₀ Q/r²

I got my equation from http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html

So the electric field at point P would have an x and y component and be equal to ______ N/C x̄, ______ N/C ŷ

Ok, but, setting a=b, that formula gives you the field normal to a line of length 2a at distance z from its midpoint.
In the present context, z is different. The z axis (where P lies, at (0, 0, h), say) is now from the middle of the rectangle and normal to it. If we consider a line (strip) of charge parallel to the y-axis (as I described in post #8), how far is P from the middle of the strip?

 

[says]

I think I was correct in post #4 then.

r = √(x²/4 + y²/4+z²
dQ = λds
dS = (x + y)/ 2

V_E = λ / 4πε₀ ⋅ dS / √r

E = -∇V_E

E = -λ / 4πε₀ ( ∂ dS/dx x̄ + ∂ dS/dy ŷ + ∂ dS/dz ẑ )

E = -λ / 4πε₀ ( [-xy-y²+4z² / (x²+y²+4z²) ] x̄ - [x²-xy+4z² / (x²+y²+4z²) ] ŷ - 4-(x-y) / (x²+y²+4z²)^3/2 ẑ

substitute into the equation:
λ: 4*10-6 C / m²
x = 0.10 m
y = 0.20 m
z = 0.10 m

E = -7.989 x̄ - 3.994 ŷ - 15.973 ẑ V/m

 

[haruspex]

r = √(x2/4 + y2/4+z2

Why the /4?

dS = (x + y)/ 2

I have no idea how you get that. How about dS=dxdy?

VE = λ / 4πε0 ⋅ dS / √r

I assume the √ is a typo.

You still don't seem to understand that you need to integrate over the area of the rectangle. If the calculation in the above post found anything it was just the field due to a point charge.

 

[says]

I found an example, which I believe is similar to my question in this document: http://mlg.eng.cam.ac.uk/mchutchon/chargedPlanes.pdf

It uses integration and Gauss' Law to find the magnitude of the electric field. I've redefined a few terms below and attempted to complete my problem again.
Ep: Electric field at point, P.
σ = charge density = 4*10^-6 C/m²
r = 10cm
x = 10cm
y = 5cm
Ep = ∫ ∫ σr / 4πε₀ sinθ dxdy
d = √ (x² + y² + r²)
sinθ = r / √ (x² + y² + r²)

Ep = σr / 4πε₀ ∫ ∫ 1 / √ (x² + y² + r²)^3/2 dxdy
Ep = σr / 4πε₀ ∫ 2 / (y² + r²)^3/2 dy
Ep = σr / 4πε₀ * 2π/r
Ep = σ / 2ε₀

The strength of the field is not dependant on how high we are above the rectangle. Anywhere above the plate and the field will be the same. The only thing the electric field at a point, P, is dependant on is the charge density, σ.

Ep = 4*10^-6 / 2(8.85*10^-12)
Ep =2.26*10⁶ N/C

 

[SammyS]

As @rude man said:

You're not following instructions which are to use the expression for the E field from a line segment as basis for the solution. Why not do it that way?

But approaching it from a potential viewpoint would certainly be possible otherwise. I did not check your math though.

You continue to ignore this instruction which appears in the given problem statement.

 

[rude man]

I think it's important that you see this the way you're supposed to. And it makes things clearer and easier to understand.

1. You were to start with just a line and a point above the line. That gave you the E field at the point. Not a hard thing to do except maybe one integration which you can solve using some math program or a table. Or you can find the solution on the Web; this part is supposed to be a "given" anyway.

2. Now you're dividing the plane into many strips like the one you just solved. The point is still above the middle of each strip; the only difference is that, as you go across the plate,
(a) the distance from each strip varies, and
(b) the direction of the E field generated by each strip also varies.

So just integrate the E field due to all the strips, taking into account the above two facts. You do not start with a differential area. You start with a differential strip.

 

[haruspex]

x = 10cm
y = 5cm

This is a confusion.
In your equations, x and y are coordinates of a general point in the plane. The 10cm and 5cm give their ranges of values (-10cm, +10cm), (-5cm, +5cm). These should become the bounds on your integrals.
The link you found is only for an infinite sheet. Yours is bounded, so the integrand is right but the bounds are different.

However you have made progress. At least now you do have a dxdy integral.

As @rude man notes, you are instructed to perform the first of the two integrations by using the known result for a finite line of charge.

 

[says]

The 10cm and 5cm give their ranges of values (-10cm, +10cm), (-5cm, +5cm). These should become the bounds on your integrals. The link you found is only for an infinite sheet. Yours is bounded, so the integrand is right but the bounds are different.

As @rude man notes, you are instructed to perform the first of the two integrations by using the known result for a finite line of charge.

Ok, so using the equation for a finite line of charge.

a: distance from the centre of the line of charge to point, P. This is given in the problem statement as 10cm=0.10m
L: half the distance of each line. So for one line of the rectangle it is 10/2 = 5cm=0.05m and the other it is 20/2 = 10cm=0.10m
λ: charge density = 4*10^-6 C/m²
k: 8.98 * 10⁹ N m² / C^-2

dE_z = kaλdx / (x² + a²)^3/2
Ez = ∫ 2kaλdx / (x² + a²)^3/2) *bounds of integration will be 0 to L. Multiplying by 2, which is in the equation.
Ez = 2kaλ ∫ dx / (x² + a²)^3/2)
Ez = 2kλL / (a√(L²+a²))

Ez = 2kλL / (a√(L²+a²))

So for the line of charge along the x-axis, L=20/2=10cm=0.10m
∴ Ez = 2 * (8.98 * 10⁹) * (4 * 10^-6) * 0.10 / (0.10√(0.10²+0.10²))
Ez = 5.08*10⁵ N/C x̄
This is the x component of the electric field at the point, P.

For the y component:
Ez = 2 * (8.98 * 10⁹) * (4 * 10^-6) * 0.05 / (0.10√(0.05²+0.10²))
Ez = 3.21*10⁵ N/C ŷ

E field at point P = 5.08*10⁵ x̄ + 3.21*10⁵ ŷ N/C

 

[haruspex]

distance from the centre of the line of charge to point, P. This is given in the problem statement as 10cm=0.10m

That given distance is from the centre of the rectangle, so it will only be from the middle of a line of charge if it is a line through the middle of the rectangle. You need to consider any line parallel to one side of the rectangle.
Draw yourself a diagram. Try to answer my question in post #10.

 

[says]

That given distance is from the centre of the rectangle, so it will only be from the middle of a line of charge if it is a line through the middle of the rectangle. You need to consider any line parallel to one side of the rectangle.
Draw yourself a diagram. Try to answer my question in post #10.

I'm a little confused with what you're trying to say here and in post #10. I've found another reference, which i believe is similar to my problem so I might look at that and then try again. ()

 

[haruspex]

I'm a little confused with what you're trying to say here and in post #10. I've found another reference, which i believe is similar to my problem so I might look at that and then try again. ()

That diagram helps, except that marking the point outside the plane as X is confusing. Let's call it P.
The "strip" I keep referring to is marked with dashed lines in the diagram.
What is the total charge on that strip?
How long is the strip?
How far is the centre of the strip from P?
If you can answer those questions you can use your formula for the field at P resulting from the strip.
However, that field has a component in the y direction. You need to extract the component in the z direction.

 

[says]

I'm a bit confused now. Even if I put different bounds in my integral in post #13, aren't I still going to end up with the same answer / equation: Ep = σ / 2ε₀?

 

[haruspex]

I'm a bit confused now. Even if I put different bounds in my integral in post #13, aren't I still going to end up with the same answer / equation: Ep = σ / 2ε₀?

No. You are leaning too heavily on the web page you found.
The lines of algebra you show in the post omit steps. To perform each integral:
step 1: find the general form of the integral for arbitrary bounds.
step 2: substitute the known bounds.
You do not show the result of step 1, and the result you show for step 2 is for the case of -∞ to +∞.

 

[says]

Ep: Electric field at point, P.
σ = charge density = 4*10-6 C/m²
r = 10cm
x = 10cm
y = 5cm
Ep = ∫ ∫ σr / 4πε0 sinθ dxdy
d = √ (x² + y² + r²)
sinθ = r / √ (x² + y² + r²)

Ep = σr / 4πε0 ∫ ∫ 1 / √ (x² + y² + r²)3/2 dxdy

I'm going to set the bounds for dx: 0, 10cm and then multiply by 2 to make it all a bit simpler.

2 ∫ 1 / (x² + y² + r²)^3/2 dx [x: from 0 to 10cm]

 

[haruspex]

x = 10cm
y = 5cm

As I wrote, that is a confusion. Those numbers give the bounds for x and y, not specific values.
Better to write -10cm < x < 10cm, etc.

2 ∫ 1 / (x2 + y2 + r2)3/2 dx [x: from 0 to 10cm]

Yes.

 

[says]

2 ∫ 1 / (x² + y² + r²)^3/2 dx [x: from 0 to 10cm]

Are there any simplifications / substitutions I can make here? The integral looks a little tricky without a calculator or tables.

 

[says]

I put the function in Wolfram and just substituted r=0.10m into the equation. If I multiply this calculation by σr / 4πε₀ then I will get the electric field at the point, P.

 

[haruspex]

2 ∫ 1 / (x² + y² + r²)^3/2 dx [x: from 0 to 10cm]

Are there any simplifications / substitutions I can make here? The integral looks a little tricky without a calculator or tables.

This is why you were told to use the standard formula for the first integration stage.
Look at the formula in the first line at http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html:

What can you substitute for the k, λ, z, a and b in there to make it match your integral?

 

[says]

k = 8.98 * 10⁹
λ = 4*10^-6
a = 0
b=0.10m
z=0.10m

Ez = 2kλz ∫ dx / (z² + x²)^3/2
Ez = 2kλ/z [ x / (z² + x²)^1/2 (evaluated from 0 to 10)
Ez = 2*8.98*10⁹*4*10^-6 / 0.10 [ 0.10 / (0.10² + 0.10²)^1/2]
Ez = 718400 / 0.70711
Ez = 1015966

 

[haruspex]

z=0.10m

No, that does not make the left hand side of the equation look like your integral.
Study my post #27. What has to replace z to make the integrand look like the one in the integral I quoted from your post?

 

[says]

The z in the hyperphysics diagram is the distance from the charge to the point P. I'm guessing the z in post #27 should be y for when we integrate dy

 

[haruspex]

The z in the hyperphysics diagram is the distance from the charge to the point P. I'm guessing the z in post #27 should be y for when we integrate dy

No need to guess. Just study the two integrals in post #27. What do you have to replace the z² inside the second integral (the one from the link) with in order to make it look like the integrand that I quoted just above it?

 

[says]

No need to guess. Just study the two integrals in post #27. What do you have to replace the z² inside the second integral (the one from the link) with in order to make it look like the integrand that I quoted just above it?

the z² inside the second integral would be y²

 

[haruspex]

the z² inside the second integral would be y²

No, that would make the integrand $(x^2+y^2)^{-\frac 32}$. You need $(x^2+y^2+r^2)^{-\frac 32}$

 

[says]

k = 8.98 * 109
λ = 4*10^-6
a = 0
b=0.10m
z = y² + r²

Ez = 2kλz ∫ dx / (z² + x²)^3/2
Ez = 2kλ/y² + r² [ x / (y² + r² + x²)^1/2] (evaluated from 0 to 10)

 

[haruspex]

z = y²+ r²

Closer.